singleRcapture: An R Package for Single-Source Capture-Recapture Models

Piotr Chlebicki, Maciej Beręsewicz

2025-01-25

Introduction

Population size estimation is a methodological approach employed across multiple scientific disciplines, which serves as the basis for research, policy formulation, and decision-making processes (cf. Böhning, Bunge, and Heijden 2018). In the field of statistics, particularly official statistics, precise population estimates are essential in order to develop robust economic models, optimize resource allocation, and inform evidence-based policy (cf. Baffour, King, and Valente 2013). Social scientists utilize advanced population estimation techniques to investigate hard-to-reach populations, such as homeless individuals or illicit drug users in an effort to overcome the inherent limitations of conventional census methodologies. These techniques are crucial for obtaining accurate data on populations that are typically under-represented or difficult to access using traditional sampling methods (cf. Vincent and Thompson 2022). In ecology and epidemiology, researchers focus on estimating the size of individual species or disease-affected populations within defined geographical regions as part of conservation efforts, ecosystem management, and public health interventions.

Population size estimation can be approached using various methodologies, each with distinct advantages and limitations. Traditional approaches include full enumeration (e.g. censuses) and comprehensive sample surveys, which, while providing detailed data, are often resource-intensive and may result in delayed estimates, particularly for human populations. Alternative methods leverage existing data sources, such as administrative registers or carefully designed small-scale studies in wildlife research, or census coverage surveys (cf. Wolter 1986; Zhang 2019). Information from these sources is often extracted by applying statistical methods, known as capture-recapture or multiple system estimation, which rely on data from multiple enumerations of the same population (cf. Dunne and Zhang 2024). This approach can be implemented using either a single source with repeated observations, two sources, or multiple sources.

In this paper we focus on methods that involve a single data source with multiple enumerations of the same units (cf. Heijden et al. 2003). In human population studies, such data can be derived from police records, health system databases, or border control logs; in the case of non-human populations, data of this kind can come from veterinary records or specialized field data. These methods are often applied to estimate hard-to-reach or hidden populations, where standard sampling methods may be inappropriate because of prohibitive costs or problems with identifying population members.

While methods for two or more sources are implemented in various open-source software packages, for instance CARE-4 (Yang and Chao 2006) (in GAUSS), Rcapture (Baillargeon and Rivest 2007), marked (Laake et al. 2013) or VGAM (Thomas W. Yee, Stoklosa, and Huggins 2015) (all in R), single-source capture-recapture (SSCR) methods are either not available at all or are only partially implemented in existing R packages or other software. Therefore, the paper attempts to bridge this gap by introducing the singleRcapture package, which implement state-of-the-art SSCR methods and offer a user friendly API resembling existing R functions (e.g., glm). In the next subsection we describe existing R packages and other software that could be used for estimating population size using SSCR methods.

Software for capture-recapture with a single source

The majority of SSCR methods assume zero-truncated distributions or their extensions (e.g., inclusion of one-inflation). The Distributions.jl (Besançon et al. 2021) (in Julia), StatsModels (Seabold and Perktold 2010) (in Python), countreg (Zeileis, Kleiber, and Jackman 2008), VGAM (T. Yee 2015) or distributions3 (Hayes et al. 2024) (in R) implement some of those truncated distributions (e.g. distributions3::ZTPoisson or countreg::zerotrunc) and the most general distributions, such as Generally Altered, Inflated, Truncated and Deflated, can be found in the VGAM package (e.g. VGAM::gaitdpoisson for the Poisson distribution, see Thomas W. Yee and Ma (2024) for a detailed description). However, the estimation of parameters of a given truncated (and possibly inflated) distribution is just the first step (as in the case of log-linear models in capture-recapture with two sources) and, to the best of our knowledge, there is no open-source software that can be used to estimate population size using on SSCR methods and includes variance estimators or diagnostics.

Therefore, the purpose of the singleRcapture, an R package, is to bridge this gap by providing scientists and other practitioners with a tool for estimating population size with SSCR methods. We have implemented state-of-the-art methods, as recently described by Böhning, Bunge, and Heijden (2018) or Böhning and Friedl (2024) and provided their extensions (e.g., inclusion of covariates, different treatment of one-inflation), which will be covered in detail in Section 2. The package implements variance estimation based on various methods, can be used to create custom models and diagnostic plots (e.g. rootograms) with parameters estimated using a modified iteratively reweighted least squares (IRLS) algorithm we have implemented for estimation stability. To the best of our knowledge, no existing open-source package allows the estimation of population size by selecting an appropriate SSCR model, conducting the estimation, and providing informative diagnostics of the results.

The remaining part of the paper is structured as follows. Section 2 contains a brief description of the theoretical background and information about fitting methods and available methods of variance estimation. Section 3 introduces the main functions of the package. Section 4 presents a case study and contains an assessment of its results, diagnostics and estimates of specific sub-populations. Section 5 describes classes and S3methods implemented in the package. The paper ends with conclusions and an appendix showing how to use the estimatePopsizeFit function which is aimed to mimic the glm.fit or similar functions. In replication materials we show how to implement a custom model as this option could be of interest to users wishing to apply any new bootstrap methods not implemented in the package.

Theoretical background

How to estimate population size with a single source?

Let $Y_{k}$ represent the number of times the $k$-th unit was observed in a single source (e.g. register). Clearly, we only observe $k:Y_{k}>0$ and do not know how many units have been missed (i.e. $Y_{k}=0$), so the population size, denoted by $N$, needs to be estimated. In general, we assume that the conditional distribution of $Y_{k}$ given a vector of covariates $\boldsymbol{x}_{k}$ follows a version of the zero-truncated count data distribution (and its extensions). When we know the parameters of the distribution we can estimate the population size using a Horvitz-Thompson type estimator given by:

$$\begin{equation} \hat{N}= \sum_{k=1}^{N}\frac{I_{k}}{\mathbb{P}[Y_{k}>0|\boldsymbol{X}_{k}]}= \sum_{k=1}^{N_{obs}}\frac{1}{\mathbb{P}[Y_{k}>0|\boldsymbol{X}_{k}]}, \end{equation}$$

where $I_{k}:=\mathcal{I}_{\mathbb{N}}(Y_{k})$, $N_{obs}$ is the number of observed units and $\mathcal{I}$ is the indicator function, while the maximum likelihood estimate of $N$ is obtained after substituting regression parameters $\boldsymbol{\beta}$ for $\mathbb{P}[Y_{k}>0|\boldsymbol{x}_{k}]$ in the above equation.

The basic SSCR assumes independence between counts, which is a rather naive assumption, since the first capture may significantly influence the behavior of a given unit or limit the possibility of subsequent captures (e.g. due to incarceration).

To solve these issues, Ryan T. Godwin and Böhning (2017b) and Ryan T. Godwin and Böhning (2017a) introduced one-inflated distributions, which explicitly model the probability of singletons by giving additional mass $\omega$ to singletons denoted as $\mathcal{I}_{\{1\}}(y)$(cf. Böhning and Friedl 2024). In other words they considered a new random varialbe $Y^{\ast}$ that corresponds to the data collection process which exhibits one inflation:

$$\begin{equation*} \mathbb{P}\left[Y^{\ast}=y|Y^{\ast}>0\right] = \omega\mathcal{I}_{\{1\}}(y)+(1-\omega)\mathbb{P}[Y=y|Y>0]. \end{equation*}$$

Analytic variance estimation is then performed by computing two parts of the decomposition according to the law of total variance given by:

$$\begin{equation}\label{eq-law_of_total_variance_decomposition} \text{var}[\hat{N}] = \mathbb{E}\left[\text{var} \left[\hat{N}|I_{1},\dots,I_{n}\right]\right] + \text{var}\left[\mathbb{E}[\hat{N}|I_{1},\dots,I_{n}]\right], \end{equation}$$

where the first part can be estimated using the multivariate $\delta$ method given by:

$$\begin{equation*} \mathbb{E}\left[\text{var} \left[\hat{N}|I_{1},\dots,I_{n}\right]\right] = \left.\left(\frac{\partial(N|I_1,\dots,I_N)}{\partial\boldsymbol{\beta}}\right)^\top \text{cov}\left[\hat{\boldsymbol{\beta}}\right] \left(\frac{\partial(N|I_1,\dots,I_N)}{\partial\boldsymbol{\beta}}\right) \right|_{\boldsymbol{\beta}=\hat{\boldsymbol{\beta}}}, \end{equation*}$$

while the second part of the decomposition above, assuming independence of $I_{k}$’s and after some omitted simplifications, is optimally estimated by:

$$\begin{equation*} \text{var}\left[\mathbb{E}(\hat{N}|I_{1},\dots,I_{n})\right] = \text{var}\left[\sum_{k=1}^{N}\frac{I_{k}}{\mathbb{P}(Y_{k}>0)}\right] \approx\sum_{k=1}^{N_{obs}}\frac{1-\mathbb{P}(Y_{k}>0)}{\mathbb{P}(Y_{k}>0)^{2}}, \end{equation*}$$

which serves as the basis for interval estimation. Confidence intervals are usually constructed under the assumption of (asymptotic) normality of $\hat{N}$ or asymptotic normality of $\ln(\hat{N}-N)$ (or log normality of $\hat{N}$). The latter is an attempt to address a common criticism of student type confidence intervals in SSCR, namely a possibly skewed distribution of $\hat{N}$, and results in the $1-\alpha$ confidence interval given by:

$$\begin{equation*} \left(N_{obs}+\frac{\hat{N}-N_{obs}}{\xi},N_{obs} + \left(\hat{N}-N_{obs}\right)\xi\right), \end{equation*}$$

where:

$$\begin{equation*} \xi = \exp\left(z\left(1-\frac{\alpha}{2}\right) \sqrt{\ln\left(1+\frac{\widehat{\text{Var}}(\hat{N})}{\left(\hat{N}-N_{obs}\right)^{2}}\right)}\right), \end{equation*}$$

and where $z$ is the quantile function of the standard normal distribution. The estimator $\hat{N}$ is best interpreted as being an estimator of the total number of units in the population, since we have no means of estimating the number of units in the population for which the probability of being included in the data is $0$(Heijden et al. 2003).

Available models

The full list of models implemented in singleRcapture along with corresponding expressions for probability density functions and point estimates can be found in the collective help file for all family functions:

?ztpoisson

For the sake of simplicity, we only list the family functions together with brief descriptions. For more detailed information, please consult the relevant literature.

The current list of these family functions includes:

• Generalized Chao’s (Chao 1987) and Zelterman’s (Zelterman 1988) estimators via logistic regression on variable $Z$ defined as $Z=1$ if $Y=2$ and $Z=0$ if $Y=1$ with $Z\sim b(p)$ where $b(\cdot)$ is the Bernoulli distribution and $p$ can be modeled for each unit $k$ by $\text{logit}(p_k)=\ln(\lambda_k/2)$ with Poisson parameter $\lambda_k=\boldsymbol{x}_{k}\boldsymbol{\beta}$ (for a covariate extension see Böhning et al. (2013) and Böhning and Heijden (2009)):

$$\hat{N}_{\text{Chao}} = N_{obs}+ \sum_{k=1}^{\boldsymbol{f}_{1}+\boldsymbol{f}_{2}} \left(2\exp\left(\boldsymbol{x}_{k}\hat{\boldsymbol{\beta}}\right)+ 2\exp\left(2\boldsymbol{x}_{k}\hat{\boldsymbol{\beta}}\right)\right)^{-1}, \tag{Chao's estimator}$$

$$\hat{N}_{\text{Zelt}}=\sum_{k=1}^{N_{obs}} \left(1-\exp\left(-2\exp\left(\boldsymbol{x}_{k}\hat{\boldsymbol{\beta}}\right)\right)\right)^{-1}. \tag{Zelterman's estimator}$$

where $\boldsymbol{f}_{1}$ and $\boldsymbol{f}_{2}$ denotes number of units observed once and twice.

• Zero-truncated (zt$^\ast$) and zero-one-truncated (zot$^\ast$) Poisson (Böhning and Heijden 2019), geometric, NB type II (NB2) regression, where the non-truncated distribution is parameterized as:

$$\mathbb{P}[Y=y|\lambda,\alpha] = \frac{\Gamma\left(y+\alpha^{-1}\right)}{\Gamma\left(\alpha^{-1}\right)y!} \left(\frac{\alpha^{-1}}{\alpha^{-1}+\lambda}\right)^{\alpha^{-1}} \left(\frac{\lambda}{\lambda + \alpha^{-1}}\right)^{y}.$$

• Zero-truncated one-inflated (ztoi$^\ast$) modifications, where the count data variable $Y^{\ast}$ is defined such that its distribution statisfies:

$$\mathbb{P}\left[Y^{\ast}=y\right]= \begin{cases} \mathbb{P}[Y=0] & y=0, \\ \omega\left(1-\mathbb{P}[Y=0]\right)+(1-\omega)\mathbb{P}[Y=1] & y=1, \\ (1-\omega)\mathbb{P}[Y=y] & y>1, \end{cases}$$

$$\mathbb{P}\left[Y^{\ast}=y|Y^{\ast}>0\right]=\omega\mathcal{I}_{\{1\}}(y)+(1-\omega)\mathbb{P}[Y=y|Y>0].$$

• One-inflated zero-truncated (oizt$^\ast$) modifications, where the count data variable $Y^{\ast}$ is defined as:

$$\mathbb{P}\left[Y^{\ast}=y\right] = \omega \mathcal{I}_{\{1\}}(y)+(1-\omega)\mathbb{P}[Y=y],$$

$$\mathbb{P}\left[Y^{\ast}=y|Y^{\ast}>0\right] = \omega\frac{\mathcal{I}_{\{1\}}(y)}{1-(1-\omega)\mathbb{P}[Y=0]}+ (1-\omega)\frac{\mathbb{P}[Y=y]}{1-(1-\omega)\mathbb{P}[Y=0]}.$$

Note that ztoi$^\ast$ and oizt$^\ast$ distributions are equivalent, in the sense that the maximum value of the likelihood function is equal for both of those distributions given any data, as shown by (Böhning 2023) but population size estimators are different.

In addition, we propose two new approaches to model singletons in a similar way as in hurdle models. In particular, we have proposed the following:

• The zero-truncated hurdle model (ztHurdle*) for Poisson, geometric and NB2 is defined as:

$$\mathbb{P}[Y^{\ast}=y]=\begin{cases} \frac{\mathbb{P}[Y=0]}{1-\mathbb{P}[Y=1]} & y=0, \\ \pi(1-\mathbb{P}[Y=1]) & y=1, \\ (1-\pi) \frac{\mathbb{P}[Y=y]}{1-\mathbb{P}[Y=1]} & y>1, \end{cases}$$

$$\mathbb{P}[Y^{\ast}=y|Y^{\ast}>0]=\pi\mathbf{1}_{\{1\}}(y)+ (1-\pi)\mathbf{1}_{\mathbb{N}\setminus\{1\}}(y)\frac{\mathbb{P}[Y=y]}{1-\mathbb{P}[Y=0]-\mathbb{P}[Y=1]}.$$

where $\pi$ denotes the conditional probability of observing singletons.

• The hurdle zero-truncated model (Hurdlezt*) for Poisson, geometric and NB2 is defined as:

$$\mathbb{P}[Y^{\ast}=y]=\begin{cases} \pi & y=1, \\ (1-\pi) \frac{\mathbb{P}[Y=y]}{1-\mathbb{P}[Y=1]} & y\neq1, \end{cases}$$

$$\mathbb{P}[Y^{\ast}=y|Y^{\ast}>0]=\begin{cases} \pi\frac{1-\mathbb{P}[Y=1]}{1-\mathbb{P}[Y=0]-\mathbb{P}[Y=1]} & y=1,\\ (1-\pi)\frac{\mathbb{P}[Y=y]}{1-\mathbb{P}[Y=0]-\mathbb{P}[Y=1]} & y>1, \end{cases}$$

where $\pi$ denotes the unconditional probability of observing singletons.

The approaches presented above differ in their assumptions, computational complexity, or in the way they treat heterogeneity of captures and singletons. For instance, the dispersion parameter $\alpha$ in the NB2 type models is often interpreted as measuring the severity of unobserved heterogeneity in the underlying Poisson process (Cruyff and Heijden 2008). When using any truncated NB model, the hope is that given the class of models considered, the consistency is not lost despite the lack of information.

While not discussed in the literature, the interpretation of heterogeneous $\alpha$ across the population (specified in controlModel) would be that the unobserved heterogeneity affects the accuracy of the prediction for the dependent variable $Y$ more severely than others. The geometric model (NB with $\alpha=1$) is singled out in the package and often considered in the literature because of inherent computational issues with NB models, which are exacerbated by the fact that data used for SSCR are usually of rather low quality. Data sparsity is a particularly common problem in SSCR and a big challenge for all numerical methods for fitting the (zero-truncated) NB model.

The extra mass $\omega$ in one-inflated models is an important extension to the researcher’s toolbox for SSCR models, since the inflation at $y=1$ is likely to occur in many types of applications. For example, when estimating the number of active people who committed criminal acts in a given time period, the fact of being captured for the first time following an arrest is associated with the risk of no longer being able to be captured a second time. One constraint present in modelling via inflated models is that attempts to include both the possibility of one inflation and one deflation lead to both numerical and inferential problems since the parameter space (of $(\omega, \lambda)$ or $(\omega, \lambda, \alpha)$) is then given by $\{(\omega, \lambda, \alpha) | \forall x\in \mathbb{N}: p(x|\omega, \lambda, \alpha)\geq0\}$ for the probability mass function $p$. The boundary of this set is then a $1$ or $2-$dimentional manifold, transforming this parameter space into $\mathbb{R}^{3}$ would require using link functions that depend on more than one parameter.

Hurdle models represent another approach to modelling one-inflation. They can also model deflation as well as inflation and deflation simultaneously, so they are more flexible and, in the case of hurdle zero-truncated models, appear to be more numerically stable.

Although the question of how to interpret regression parameters tends to be somewhat overlooked in SSCR studies, we should point out that the interpretation of the $\omega$ inflation parameter (in ztoi$^\ast$ or oizt$^\ast$) is more convenient than the interpretation of the $\pi$ probability parameter (in hurdle models). Additionally, the interpretation of the $\lambda$ parameter in (one) inflated models conforms to the following intuition: given that unit $k$ comes from the non-inflated part of the population, it follows a Poisson distribution (respectively geometric or negative binomial) with the $\lambda$ parameter (or $\lambda,\alpha$); no such interpretation exists for hurdle models. Interestingly, estimates from hurdle zero-truncated and one-inflated zero-truncated models tend to be quite close to one another, although more rigorous studies are required to confirm this observation.

Fitting method

As previously noted, the singleRcapture package can be used to model the (linear) dependence of all parameters on covariates. A modified IRLS algorithm is employed for this purpose as presented in Algorithm 1; full details are available in T. Yee (2015). In order to apply the algorithm, a modified model matrix $\boldsymbol{X}_{\text{vlm}}$ is created when the estimatePopsize function is called. In the context of the models implemented in singleRcapture, this matrix can be written as:

$$ \begin{equation}\label{X_vlm-definition} \boldsymbol{X}_{\text{vlm}}= \begin{pmatrix} \boldsymbol{X}_{1} & \boldsymbol{0}&\dotso &\boldsymbol{0}\cr \boldsymbol{0}& \boldsymbol{X}_{2} &\dotso &\boldsymbol{0}\cr \vdots & \vdots & \ddots & \vdots\cr \boldsymbol{0}& \boldsymbol{0}&\dotso &\boldsymbol{X}_{p} \end{pmatrix} \end{equation} $$

where each $\boldsymbol{X}_{i}$ corresponds to a model matrix associated with a user specified formula.

Algorithm 1: The modified IRLS algorithm used in the singleRcapture package

1. Initialize with iter ← 1, $\boldsymbol{\eta}$ ← start, $\boldsymbol{W}$ ← I, $\ell$ ← $\ell(\boldsymbol{\beta})$

2. Store values from the previous step:
   $\ell_{-}$ ← $\ell$, $\boldsymbol{W}_{-}$ ← $\boldsymbol{W}$, $\boldsymbol{\beta}_{-}$ ← $\boldsymbol{\beta}$ (the last assignment is omitted during the first iteration), and assign values in the current iteration:

   $\displaystyle\boldsymbol{\eta}$ ← $\boldsymbol{X}_{\text{vlm}}\boldsymbol{\beta}+\boldsymbol{o}$

   $\boldsymbol{W}_{(k)}$ ← $\mathbb{E}\left[-\frac{\partial^{2}\ell}{\partial\boldsymbol{\eta}_{(k)}^\top\partial\boldsymbol{\eta}_{(k)}}\right]$

   $\boldsymbol{Z}_{(k)}$ ← $\boldsymbol{\eta}_{(k)}+\frac{\partial\ell}{\partial\boldsymbol{\eta}_{(k)}}\boldsymbol{W}_{(k)}^{-1}-\boldsymbol{o}_{(k)}$

   where $\boldsymbol{o}$ denotes offset.

3. Assign the current coefficient value:
   $\boldsymbol{\beta}$ ← $\left(\boldsymbol{X}_{\text{vlm}}\boldsymbol{W}\boldsymbol{X}_{\text{vlm}}\right)^{-1}\boldsymbol{X}_{\text{vlm}}\boldsymbol{W}\boldsymbol{Z}$

4. If $\ell(\boldsymbol{\beta})<\ell(\boldsymbol{\beta}_{-})$ try selecting the smallest value $h$ such that for $\boldsymbol{\beta}_{h}$ ← $2^{-h}\left(\boldsymbol{\beta}+\boldsymbol{\beta}_{-}\right)$ the inequality $\ell(\boldsymbol{\beta}_{h})>\ell(\boldsymbol{\beta}_{-})$ holds if this is successful $\boldsymbol{\beta}$ ← $\boldsymbol{\beta}_{h}$, else stop the algorithm.

5. If convergence is achieved or iter is higher than maxiter, stop the algorithm, else iter ← 1 + iter and return to step 2.

In the case of multi-parameter families, we get a matrix of linear predictors $\boldsymbol{\eta}$ instead of a vector, with the number of columns matching the number of parameters in the distribution. “Weights” (matrix $\boldsymbol{W}$) are then modified to be information matrices $\displaystyle\mathbb{E}\left[-\frac{\partial^{2}\ell}{\partial\boldsymbol{\eta}_{(k)}^\top\partial\boldsymbol{\eta}_{(k)}}\right]$, where $\ell$ is the log-likelihood function and $\boldsymbol{\eta}_{(k)}$ is the $k$-th row of $\boldsymbol{\eta}$, while in the typical IRLS they are scalars $\displaystyle\mathbb{E}\left[-\frac{\partial^{2}\ell}{\partial\eta_{k}^{2}}\right]$, which is often just $\displaystyle-\frac{\partial^{2}\ell}{\partial\eta^{2}}$.

Bootstrap variance estimators

We have implemented three types of bootstrap algorithms: parametric (adapted from theory in Zwane and Van der Heijden (2003), Norris and Pollock (1996) for multiple source setting with covariates), semi-parametric (see e.g. Böhning and Friedl (2021)) and nonparametric. The nonparametric version is the usual bootstrap algorithm; which will typically underestimate the variance of $\hat{N}$. In this section, the focus is on the first two approaches.

The idea of semi-parametric bootstrap is to modify the usual bootstrap to include the additional uncertainty resulting from the fact that the sample size is a random variable. This type of bootstrap is performed in steps listed in Algorithm 2.

Algorithm 2: Semi-parametric bootstrap

1. Draw a sample of size $N_{obs}'\sim\text{Binomial}\left(N', \frac{N_{obs}}{N'}\right)$, where $N'=\lfloor\hat{N}\rfloor+\text{Bernoulli}\left(\lfloor\hat{N}\rfloor-\hat{N}\right)$
2. Draw $N_{obs}'$ units from the data uniformly without replacement
3. Obtain a new population size estimate $N_b$ using bootstrap data
4. Repeat 1-3 steps $B$ times

In other words, we first draw a sample size and then a sample conditional on the sample size. Note that when using the semi-parametric bootstrap one implicitly assumes that the population size estimate $\hat{N}$ is accurate. The last implemented bootstrap type is the parametric algorithm, which first draws a finite population of size $\approx\hat{N}$ from the superpopulation model and then samples from this population according to the selected model, as described in Algorithm 3.

Algorithm 3: Parametric bootstrap

1. Draw the number of covariates equal to $\lfloor\hat{N}\rfloor+\text{Bernoulli}\left(\lfloor\hat{N}\rfloor-\hat{N}\right)$ proportional to the estimated contribution $(\mathbb{P}\left[Y_{k}>0|\boldsymbol{x}_{k}\right])^{-1}$ with replacement
2. Using the fitted model and regression coefficients $\hat{\boldsymbol{\beta}}$ draw for each covariate the $Y$ value from the corresponding probability measure on $\mathbb{N}\cup\{0\}$
3. Truncate units with the drawn $Y$ value equal to $0$
4. Obtain a population size estimate $N_b$ based on the truncated data
5. Repeat 1-4 steps $B$ times

Note that in order for this type of algorithm to result in consistent standard error estimates, it is imperative that the estimated model for the entire superpopulation probability space is consistent, which may be much less realistic than in the case of the semi-parametric bootstrap. The parametric bootstrap algorithm is the default option in singleRcapture.

The main function

The estimatePopsize function

The singleRcapture package is built around the estimatePopsize function. The main design objective was to make using estimatePopsize as similar as possible to the standard stats::glm function or packages for fitting zero-truncated regression models, such as countreg (e.g. countreg::zerotrunc function). The estimatePopsize function is used to first fit an appropriate (vector) generalized linear model and to estimate the population size along with its variance. It is assumed that the response vector (i.e. the dependent variable) corresponds to the number of times a given unit was observed in the source. The most important arguments are given in Table below; the obligatory ones are formula, data, model.

Argument	Description
formula	The main formula (i.e., for the Poisson $\lambda$ parameter);
data	A data.frame (or data.frame coercible) object;
model	Either a function, a string, or a family class object specifying which model should be used; possible values are listed in the documentation. The supplied argument should have the form model = "ztpoisson", model = ztpoisson, or if a link function should be specified, then model = ztpoisson(lambdaLink = "log") can be used;
method	A numerical method used to fit regression IRLS or optim;
popVar	A method for estimating variance of $\hat{N}$ and creating confidence intervals (either bootstrap, analytic, or skipping the estimation entirely);
controlMethod, controlModel, or controlPopVar	Control parameters for numerical fitting, specifying additional formulas (inflation, dispersion) and population size estimation, respectively;
offset	A matrix of offset values with the number of columns matching the number of distribution parameters, providing offset values to each of the linear predictors;
...	Additional optional arguments passed to other methods, e.g., estimatePopsizeFit;

An important step in using estimatePopsize is specifying the model parameter, which indicates the type of model that will be used for estimating the unobserved part of the population. For instance, to fit Chao’s or Zelterman’s model one should select chao or zelterman and, assuming that one-inflation is present, one can select one of the zero-truncated one-inflated (ztoi$^\ast$) or one-inflated zero-truncated (oizt$^\ast$) models, such as oiztpoisson for Poisson or ztoinegbin for NB2.

If it is assumed that heterogeneity is observed for NB2 models, one can specify the formula in the controlModel argument with the controlModel function and the alphaFormula argument. This enables the user to provide a formula for the dispersion parameter in the NB2 models. If heterogeneity is assumed for ztoi$^\ast$ or oizt$^\ast$, one can specify the omegaFormula argument, which corresponds to the $\omega$ parameter in these models. Finally, if covariates are assumed to be available for the hurdle models (ztHurdle$^\ast$ or Hurdlezt$^\ast$), then piFormula can be specified, as it provides a formula for the probability parameter in these models.

Controlling variance estimation with controlPopVar

The estimatePopsize function makes it possible to specify the variance estimation method via popVar (e.g. analytic or variance bootstrap) and control the estimation process by specifying controlPopVar. In the control function controlPopVar the user can specify the bootType argument, which has three possible values: "parametric", "semiparametric" and "nonparametric". Additional arguments accepted by the contorlPopVar function, which are relevant to bootstrap, include:

• alpha, B – the significance level and the number of bootstrap samples to be performed, respectively, with $0.05$ and $500$ being the default options.
• cores – the number of process cores to be used in bootstrap (1 by default); parallel computing is enabled by doParallel (Microsoft and Weston 2022a), foreach (Microsoft and Weston 2022b) and parallel packages (R Core Team 2023).
• keepbootStat – a logical value indicating whether to keep a vector of statistics produced by the bootstrap.
• traceBootstrapSize, bootstrapVisualTrace – logical values indicating whether sample and population size should be tracked (FALSE by default); these work only when cores = 1.
• fittingMethod, bootstrapFitcontrol – the fitting method (by default the same as the one used in the original call) and control parameters (controlMethod) for model fitting in the bootstrap.

In addition, the user can specify the type of confidence interval by means of confType and the type of covariance matrix by using covType for the analytical variance estimator (observed or the Fisher information matrix).

In the next sections we present a case study involving the use of a simple zero-truncated Poisson regression and a more advanced model: one-inflated zero-truncated geometric regression with the cloglog link function. First, we present the example dataset, then we describe how to estimate the population size and assess the quality and diagnostics measures. Finally, we show how to estimate the population size in user-specified sub-populations.

Data analysis example

The package can be installed in the standard manner using:

install.packages("singleRcapture")

Then, we need to load the package using the following code:

library(singleRcapture)

Dataset

We use a dataset from Heijden et al. (2003), which contains information about immigrants in four Dutch cities (Amsterdam, Rotterdam, The Hague and Utrecht), who were staying in the country without a legal permit in 1995 and appeared in police records for that year. This dataset is included in the package called netherlandsimmigrant:

data(netherlandsimmigrant)
head(netherlandsimmigrant)

##   capture gender    age       reason       nation
## 1       1   male <40yrs Other reason North Africa
## 2       1   male <40yrs Other reason North Africa
## 3       1   male <40yrs Other reason North Africa
## 4       1   male <40yrs Other reason         Asia
## 5       1   male <40yrs Other reason         Asia
## 6       2   male <40yrs Other reason North Africa

The number of times each individual appeared in the records is included in the capture variable. The available covariates include gender, age, reason, nation; the last two represent the reason for being captured and the region of the world a given person comes from:

summary(netherlandsimmigrant)

##     capture         gender         age                reason    
##  Min.   :1.000   female: 398   <40yrs:1769   Illegal stay: 259  
##  1st Qu.:1.000   male  :1482   >40yrs: 111   Other reason:1621  
##  Median :1.000                                                  
##  Mean   :1.162                                                  
##  3rd Qu.:1.000                                                  
##  Max.   :6.000                                                  
##                     nation    
##  American and Australia: 173  
##  Asia                  : 284  
##  North Africa          :1023  
##  Rest of Africa        : 243  
##  Surinam               :  64  
##  Turkey                :  93

One notable characteristic of this dataset is that it contains a disproportionately large number of individuals who were observed only once (i.e. 1645).

table(netherlandsimmigrant$capture)

## 
##    1    2    3    4    5    6 
## 1645  183   37   13    1    1

The basic syntax of estimatePopsize is very similar to that of glm, the same can be said about the output of the summary method except for additional results of population size estimates (denoted as Population size estimation results).

basicModel <- estimatePopsize(
  formula = capture ~ gender + age + nation,
  model   = ztpoisson(),
  data    = netherlandsimmigrant,
  controlMethod = controlMethod(silent = TRUE)
)
summary(basicModel)

## 
## Call:
## estimatePopsize.default(formula = capture ~ gender + age + nation, 
##     data = netherlandsimmigrant, model = ztpoisson(), controlMethod = controlMethod(silent = TRUE))
## 
## Pearson Residuals:
##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -0.486442 -0.486442 -0.298080  0.002093 -0.209444 13.910844 
## 
## Coefficients:
## -----------------------
## For linear predictors associated with: lambda 
##                      Estimate Std. Error z value  P(>|z|)    
## (Intercept)           -1.3411     0.2149  -6.241 4.35e-10 ***
## gendermale             0.3972     0.1630   2.436 0.014832 *  
## age>40yrs             -0.9746     0.4082  -2.387 0.016972 *  
## nationAsia            -1.0926     0.3016  -3.622 0.000292 ***
## nationNorth Africa     0.1900     0.1940   0.979 0.327398    
## nationRest of Africa  -0.9106     0.3008  -3.027 0.002468 ** 
## nationSurinam         -2.3364     1.0136  -2.305 0.021159 *  
## nationTurkey          -1.6754     0.6028  -2.779 0.005445 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## AIC: 1712.901
## BIC: 1757.213
## Residual deviance: 1128.553
## 
## Log-likelihood: -848.4504 on 1872 Degrees of freedom 
## Number of iterations: 8
## -----------------------
## Population size estimation results: 
## Point estimate 12690.35
## Observed proportion: 14.8% (N obs = 1880)
## Std. Error 2808.169
## 95% CI for the population size:
##           lowerBound upperBound
## normal      7186.444   18194.26
## logNormal   8431.275   19718.32
## 95% CI for the share of observed population:
##           lowerBound upperBound
## normal     10.332927   26.16037
## logNormal   9.534281   22.29793

The output regarding the population size contains the point estimate, the observed proportion (based on the input dataset), the standard error and two confidence intervals: one relating to the point estimate, the second – to the observed proportion.

According to this simple model, the population size is about 12,500, with about 15% of units observed in the register. The 95% CI under normality indicates that the true population size is likely to be between 7,000-18,000, with about 10-26% of the target population observed in the register.

Since there is a reasonable suspicion that the act of observing a unit in the dataset may lead to undesirable consequences for the person concerned (in this case, a possible deportation, detention or something similar). For these reasons, the user may consider one-inflated models, such as one-inflated zero-truncated geometric model (specified by oiztgeom family) and those presented below.

set.seed(123456)
modelInflated <- estimatePopsize(
    formula = capture ~ nation,
    model   = oiztgeom(omegaLink = "cloglog"),
    data    = netherlandsimmigrant,
    controlModel = controlModel(
        omegaFormula = ~ gender + age
    ),
    popVar = "bootstrap",
    controlPopVar = controlPopVar(bootType = "semiparametric",
                                  B = 50)
)
summary(modelInflated)

## 
## Call:
## estimatePopsize.default(formula = capture ~ nation, data = netherlandsimmigrant, 
##     model = oiztgeom(omegaLink = "cloglog"), popVar = "bootstrap", 
##     controlModel = controlModel(omegaFormula = ~gender + age), 
##     controlPopVar = controlPopVar(bootType = "semiparametric", 
##         B = 50))
## 
## Pearson Residuals:
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -0.41643 -0.41643 -0.30127  0.00314 -0.18323 13.88376 
## 
## Coefficients:
## -----------------------
## For linear predictors associated with: lambda 
##                      Estimate Std. Error z value  P(>|z|)    
## (Intercept)           -1.2552     0.2149  -5.840 5.22e-09 ***
## nationAsia            -0.8193     0.2544  -3.220  0.00128 ** 
## nationNorth Africa     0.2057     0.1838   1.119  0.26309    
## nationRest of Africa  -0.6692     0.2548  -2.627  0.00862 ** 
## nationSurinam         -1.5205     0.6271  -2.425  0.01532 *  
## nationTurkey          -1.1888     0.4343  -2.737  0.00619 ** 
## -----------------------
## For linear predictors associated with: omega 
##             Estimate Std. Error z value  P(>|z|)    
## (Intercept)  -1.4577     0.3884  -3.753 0.000175 ***
## gendermale   -0.8738     0.3602  -2.426 0.015267 *  
## age>40yrs     1.1745     0.5423   2.166 0.030326 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## AIC: 1677.125
## BIC: 1726.976
## Residual deviance: 941.5416
## 
## Log-likelihood: -829.5625 on 3751 Degrees of freedom 
## Number of iterations: 10
## -----------------------
## Population size estimation results: 
## Point estimate 6699.953
## Observed proportion: 28.1% (N obs = 1880)
## Boostrap sample skewness: 0.5209689
## 0 skewness is expected for normally distributed variable
## ---
## Bootstrap Std. Error 1579.235
## 95% CI for the population size:
## lowerBound upperBound 
##   5107.533  10738.242 
## 95% CI for the share of observed population:
## lowerBound upperBound 
##   17.50752   36.80838

According to this approach, the population size is about 7,000, which is about 5,000 less than in the case of the naive Poisson approach. A comparison of AIC and BIC suggests that the one-inflation model fits the data better with BIC for oiztgeom 1727 and 1757 for ztpoisson.

We can access population size estimates using the following code, which returns a list with numerical results.

popSizeEst(basicModel)    # alternative: basicModel$populationSize

## Point estimate: 12690.35
## Variance: 7885812
## 95% confidence intervals:
##           lowerBound upperBound
## normal      7186.444   18194.26
## logNormal   8431.275   19718.32

popSizeEst(modelInflated) # alternative: modelInflated$populationSize

## Point estimate: 6699.953
## Variance: 2493985
## 95% confidence intervals:
## lowerBound upperBound 
##   5107.533  10738.242

The decision whether to use a zero-truncated Poisson or one-inflated zero-truncated geometric model should be based on the assessment of the model and the assumptions regarding the data generation process. One possible method of selection is based on the likelihood ratio test, which can be computed quickly and conveniently with the lmtest (Zeileis and Hothorn (2002)) interface:

library(lmtest)

lrtest(basicModel, modelInflated, 
       name = function(x) {
    if (family(x)$family == "ztpoisson")
        "Basic model"
    else "Inflated model"
})

## Likelihood ratio test
## 
## Model 1: Basic model
## Model 2: Inflated model
##   #Df  LogLik Df  Chisq Pr(>Chisq)    
## 1   8 -848.45                         
## 2   9 -829.56  1 37.776  7.936e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

However, the above is not a standard method of model selection in SSCR. The next sections are dedicated to a detailed description of how to assess the results using standard statistical tests and diagnostics.

Testing marginal frequencies

A popular method of testing the model fit in single source capture-recapture studies consists in comparing the fitted marginal frequencies $\displaystyle\sum_{j=1}^{N_{obs}}\hat{\mathbb{P}}\left[Y_{j}=k|\boldsymbol{x}_{j}, Y_{j} > 0\right]$ with the observed marginal frequencies $\displaystyle\sum_{j=1}^{N}\mathcal{I}_{\{k\}}(Y_{j})=\sum_{j=1}^{N_{obs}}\mathcal{I}_{\{k\}}(Y_{j})$ for $k\geq1$. If the fitted model bears sufficient resemblance to the real data collection process, these quantities should be quite close and both $G$ and $\chi^{2}$ tests can be used to test the statistical significance of the discrepancy with the following singleRcapture syntax for the Poisson model (rather poor fit):

margFreq <- marginalFreq(basicModel)
summary(margFreq, df = 1, dropl5 = "group")

## Test for Goodness of fit of a regression model:
## 
##                  Test statistics df P(>X^2)
## Chi-squared test           50.06  1 1.5e-12
## G-test                     34.31  1 4.7e-09
## 
## -------------------------------------------------------------- 
## Cells with fitted frequencies of < 5 have been grouped 
## Names of cells used in calculating test(s) statistic: 1 2 3

and for the one-inflated model (better fit):

margFreq_inf <- marginalFreq(modelInflated)
summary(margFreq_inf, df = 1, dropl5 = "group")

## Test for Goodness of fit of a regression model:
## 
##                  Test statistics df P(>X^2)
## Chi-squared test            1.88  1    0.17
## G-test                      2.32  1    0.13
## 
## -------------------------------------------------------------- 
## Cells with fitted frequencies of < 5 have been grouped 
## Names of cells used in calculating test(s) statistic: 1 2 3 4

where the dropl5 argument is used to indicate how to handle cells with less than $5$ fitted observations. Note, however, that currently there is no continuity correction.

Diagnostics

The singleRStaticCountData class has a plot method implementing several types of quick demonstrative plots, such as the rootogram (Kleiber and Zeileis 2016), for comparing fitted and marginal frequencies, which can be generated with the following syntax:

plot(   basicModel, plotType = "rootogram", main = "ZT Poisson model")
plot(modelInflated, plotType = "rootogram", main = "OI ZT Geometric model")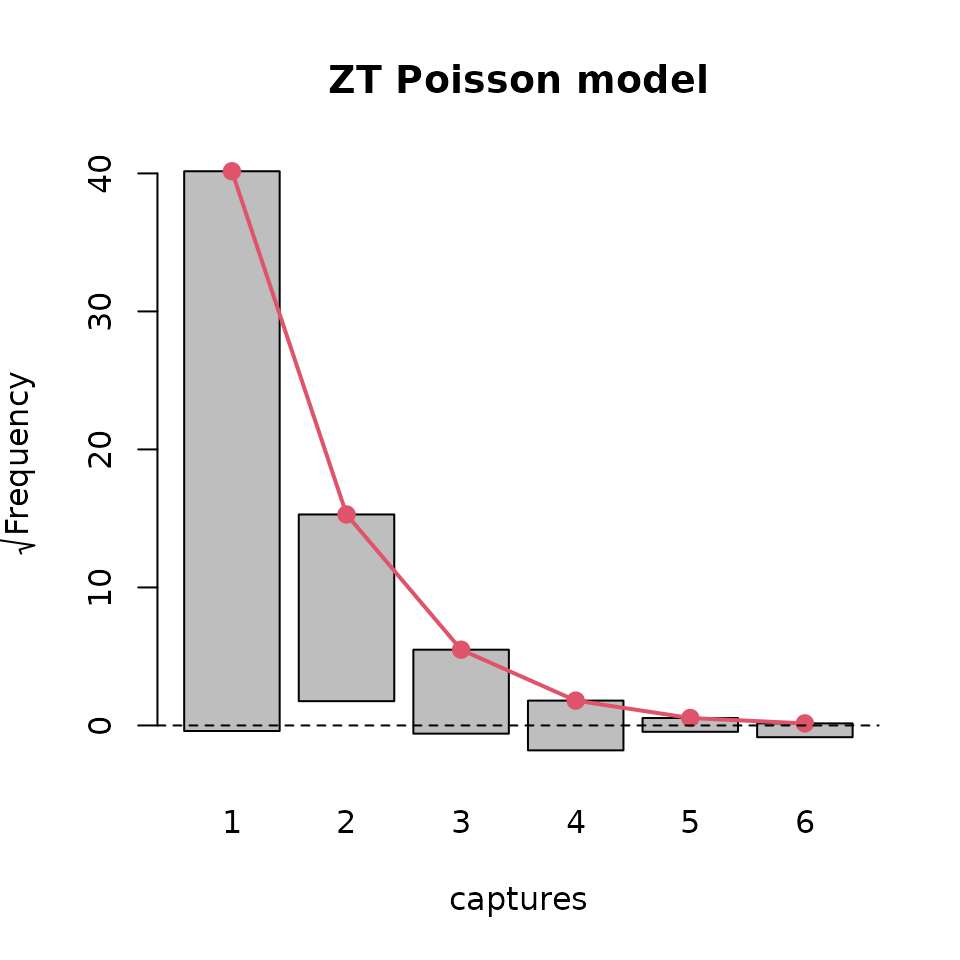

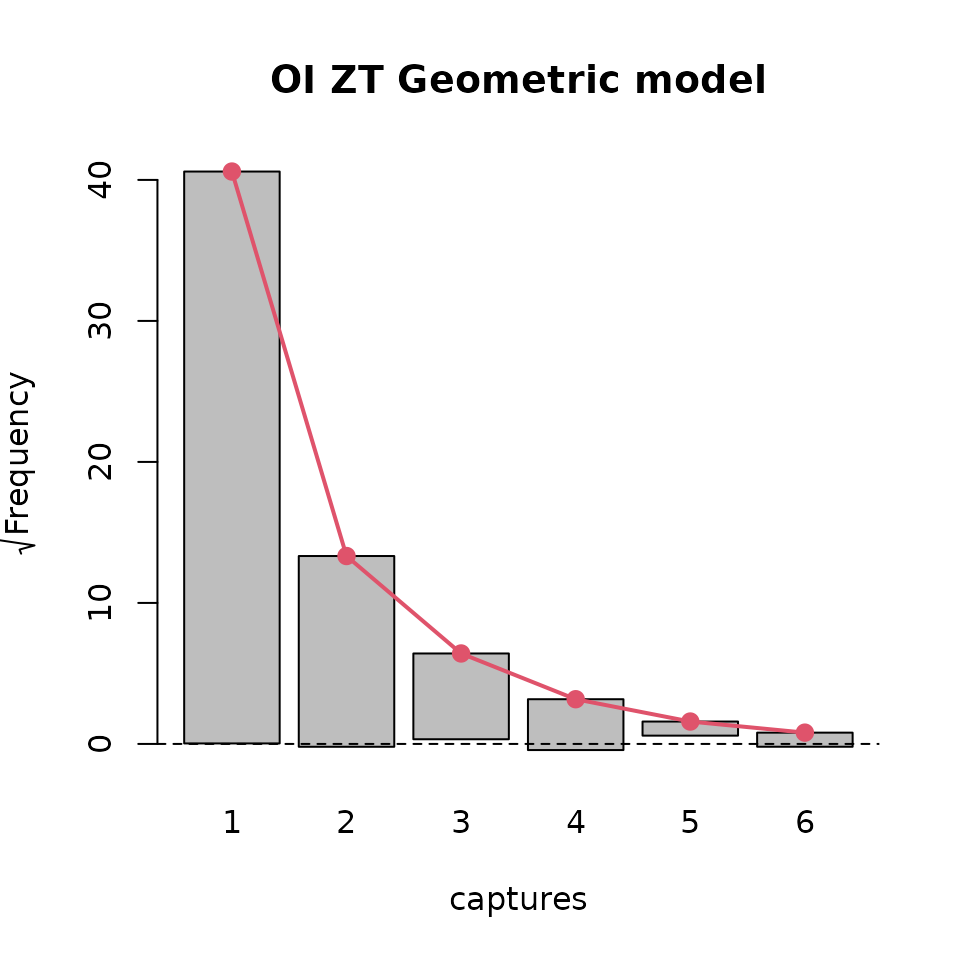
Rootograms for ztpoisson (left) and oiztgeom (right) models

The above plots suggest that the oiztgeom model fits the data better. Another important issue in population size estimation is to conduct model diagnostics in order to verify whether influential observations are present in the data. For this purpose the leave-one-out (LOO) diagnostic implemented in the dfbeta from the stats package has been adapted as shown below (multiplied by a factor of a hundred for better readability):

dfb <- dfbeta(basicModel)
round(t(apply(dfb, 2, quantile)*100), 4)

##                           0%     25%     50%    75%    100%
## (Intercept)          -0.9909 -0.1533  0.0191 0.0521  8.6619
## gendermale           -9.0535 -0.0777 -0.0283 0.1017  2.2135
## age>40yrs            -2.0010  0.0179  0.0379 0.0691 16.0061
## nationAsia           -9.5559 -0.0529  0.0066 0.0120 17.9914
## nationNorth Africa   -9.6605 -0.0842 -0.0177 0.0087  3.1260
## nationRest of Africa -9.4497 -0.0244  0.0030 0.0083 10.9787
## nationSurinam        -9.3140 -0.0066  0.0020 0.0035 99.3383
## nationTurkey         -9.6198 -0.0220  0.0079 0.0143 32.0980

dfi <- dfbeta(modelInflated)
round(t(apply(dfi, 2, quantile)*100), 4)

##                            0%     25%     50%     75%    100%
## (Intercept)           -1.4640  0.0050  0.0184  0.0557  9.0600
## nationAsia            -6.6331 -0.0346  0.0157  0.0347 12.2406
## nationNorth Africa    -7.2770 -0.0768 -0.0170  0.0085  1.9415
## nationRest of Africa  -6.6568 -0.0230  0.0081  0.0262  7.1710
## nationSurinam         -6.2308 -0.0124  0.0162  0.0421 62.2045
## nationTurkey          -6.4795 -0.0273  0.0204  0.0462 21.1338
## (Intercept):omega     -6.8668 -0.0193  0.0476  0.0476  9.3389
## gendermale:omega      -2.2733 -0.2227  0.1313  0.2482 11.1234
## age>40yrs:omega      -30.2130 -0.2247 -0.1312 -0.0663  2.0393

The result of the dfbeta can be further used in the dfpopsize function, which can be used to quantify LOO on the population size. Note the warning when the bootstap variance estimation is applied.

dfb_pop <- dfpopsize(basicModel, dfbeta = dfb)
dfi_pop <- dfpopsize(modelInflated, dfbeta = dfi)
summary(dfb_pop)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -4236.412     2.664     2.664     5.448    17.284   117.448

summary(dfi_pop)

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## -456.6443   -3.1121   -0.7243    3.4333    5.1535  103.5949

Figure 2 shows a comparison of the effect of deleting an observation on the population size estimate and inverse probability weights, which refer to the contribution of a given observation to the population size estimate:

plot(basicModel, plotType = "dfpopContr", 
     dfpop = dfb_pop, xlim = c(-4500, 150))
plot(modelInflated, plotType = "dfpopContr", 
     dfpop = dfi_pop, xlim = c(-4500, 150))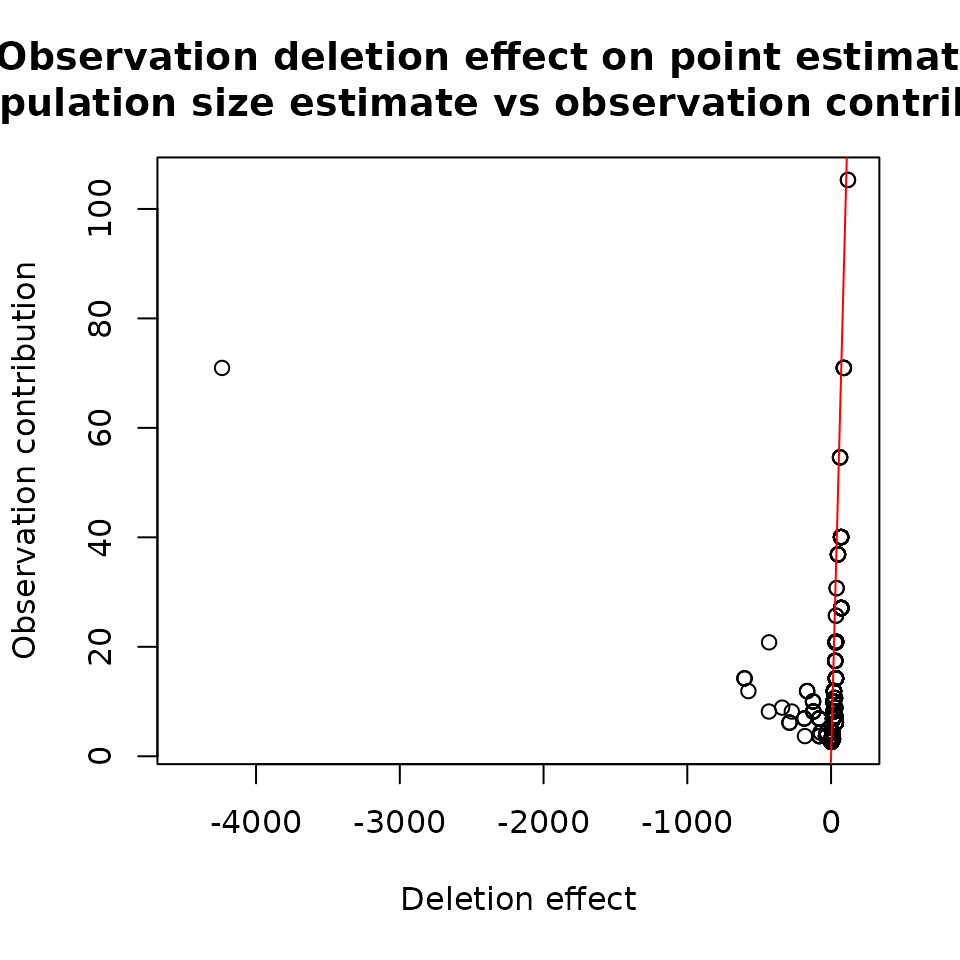

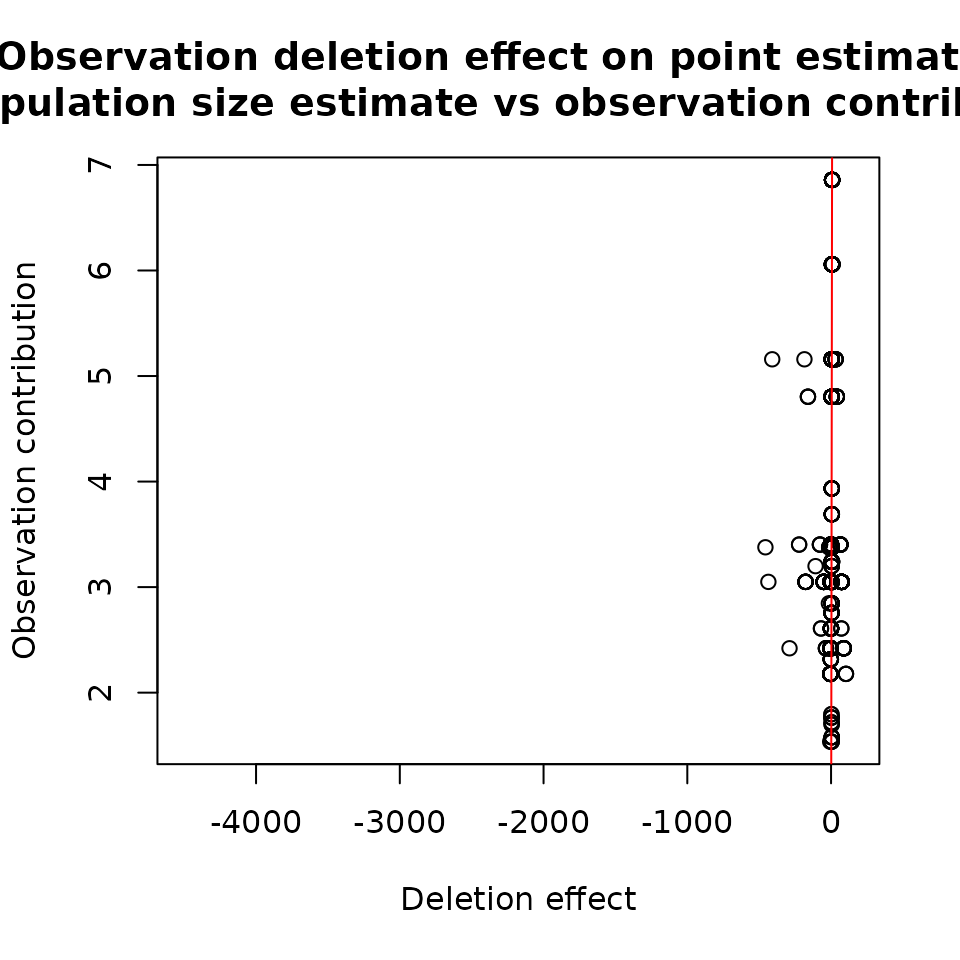
Results for ztpoisson (left) and oiztgeom (right) model

These plots show how the population size changes if a given observation is removed. For instance, if we remove observation 542, then the population size will increase by about 4236 for the ztpoisson model. In the case of oiztgeom, the largest change is equal to 457 for observation 900.

The full list of plot types along with the list of optional arguments that can be passed from the call to the plot method down to base R and graphics functions can be found in the help file of the plot method.

?plot.singleRStaticCountData

The stratifyPopsize function

Researchers may be interested not only in the total population size but also in the size of specific sub-populations (e.g. males, females, particular age groups). For this reason we have created the stratifyPopsize function, which estimates the size by strata defined by the coefficients in the model (the default option). The following output presents results based on the ztpoisson and oiztgeom models.

popSizestrata <- stratifyPopsize(basicModel)
cols <- c("name", "Observed", "Estimated", "logNormalLowerBound", 
          "logNormalUpperBound")
popSizestrata_report <- popSizestrata[, cols]
cols_custom <- c("Name", "Obs", "Estimated", "LowerBound", "UpperBound")
names(popSizestrata_report) <- cols_custom
popSizestrata_report

##                              Name  Obs  Estimated LowerBound UpperBound
## 1                  gender==female  398  3811.0924  2189.0439   6902.140
## 2                    gender==male 1482  8879.2613  6090.7752  13354.889
## 3                     age==<40yrs 1769 10506.8994  7359.4140  15426.465
## 4                     age==>40yrs  111  2183.4543   872.0130   5754.881
## 5  nation==American and Australia  173   708.3688   504.6086   1037.331
## 6                    nation==Asia  284  2742.3147  1755.2548   4391.590
## 7            nation==North Africa 1023  3055.2033  2697.4900   3489.333
## 8          nation==Rest of Africa  243  2058.1533  1318.7466   3305.786
## 9                 nation==Surinam   64  2386.4544   505.2460  12288.008
## 10                 nation==Turkey   93  1739.8592   638.0497   5068.959

popSizestrata_inflated <- stratifyPopsize(modelInflated)
popSizestrata_inflated_report <- popSizestrata_inflated[, cols]
names(popSizestrata_inflated_report) <- cols_custom
popSizestrata_inflated_report

##                              Name  Obs Estimated LowerBound UpperBound
## 1  nation==American and Australia  173  516.2432   370.8463   768.4919
## 2                    nation==Asia  284 1323.5377   831.1601  2258.9954
## 3            nation==North Africa 1023 2975.8801  2254.7071  4119.3050
## 4          nation==Rest of Africa  243 1033.9753   667.6106  1716.4484
## 5                 nation==Surinam   64  354.2236   193.8891   712.4739
## 6                  nation==Turkey   93  496.0934   283.1444   947.5309
## 7                  gender==female  398 1109.7768   778.7197  1728.7066
## 8                    gender==male 1482 5590.1764  3838.4550  8644.0776
## 9                     age==<40yrs 1769 6437.8154  4462.3472  9862.2147
## 10                    age==>40yrs  111  262.1379   170.9490   492.0347

The stratifyPopsize function prepared to handle objects of the singleRStaticCountData class, accepts three optional parameters strata, alpha, cov, which are used for specifying sub-populations, significance levels and the covariance matrix to be used for computing standard errors. An example of the full call is presented below.

library(sandwich)
popSizestrataCustom <- stratifyPopsize(
  object  = basicModel,
  strata = ~ gender + age, 
  alpha   = rep(c(0.1, 0.05), each=2), 
  cov     = vcovHC(basicModel, type = "HC4")
)

popSizestrataCustom_report <- popSizestrataCustom[, c(cols, "confLevel")]
names(popSizestrataCustom_report) <- c(cols_custom, "alpha")
popSizestrataCustom_report

##             Name  Obs Estimated LowerBound UpperBound alpha
## 1 gender==female  398  3811.092  2275.6410   6602.168  0.10
## 2   gender==male 1482  8879.261  6261.5109  12930.760  0.10
## 3    age==<40yrs 1769 10506.899  7297.2057  15580.151  0.05
## 4    age==>40yrs  111  2183.454   787.0673   6464.016  0.05

We have provided integration with the sandwich (Zeileis, Köll, and Graham 2020) package to correct the variance-covariance matrix in the $\delta$ method. In the code we have used the vcovHC method for singleRStaticCountData class from the sandwich package, different significance levels for confidence intervals in each stratum and a formula to specify that we want estimates for both males and females to be grouped by nation and age. The strata parameter can be specified either as:

• a formula with the empty left hand side, as shown in the example above (e.g. ~ gender * age),
• a logical vector with the number of entries equal to the number of rows in the dataset, in which case only one stratum will be created (e.g. netherlandsimmigrant$gender == "male"),
• a vector of names of explanatory variables, which will result in every level of the explanatory variable having its own sub-population for each variable specified (e.g. c("gender", "age")),
• not supplied at all, in which case strata will correspond to levels of each factor in the data without any interactions (string vectors will be converted to factors for the convenience of the user),
• a (named) list where each element is a logical vector; names of the list will be used to specify variable names in the returned object, for example:

list(
  "Stratum 1" = netherlandsimmigrant$gender == "male"   & 
    netherlandsimmigrant$nation == "Suriname", 
  "Stratum 2" = netherlandsimmigrant$gender == "female" & 
    netherlandsimmigrant$nation == "North Africa"
)

One can also specify plotType = "strata" in the plot function, which results in a plot with point and CI estimates of the population size.

plot(basicModel, plotType = "strata")
plot(modelInflated, plotType = "strata")

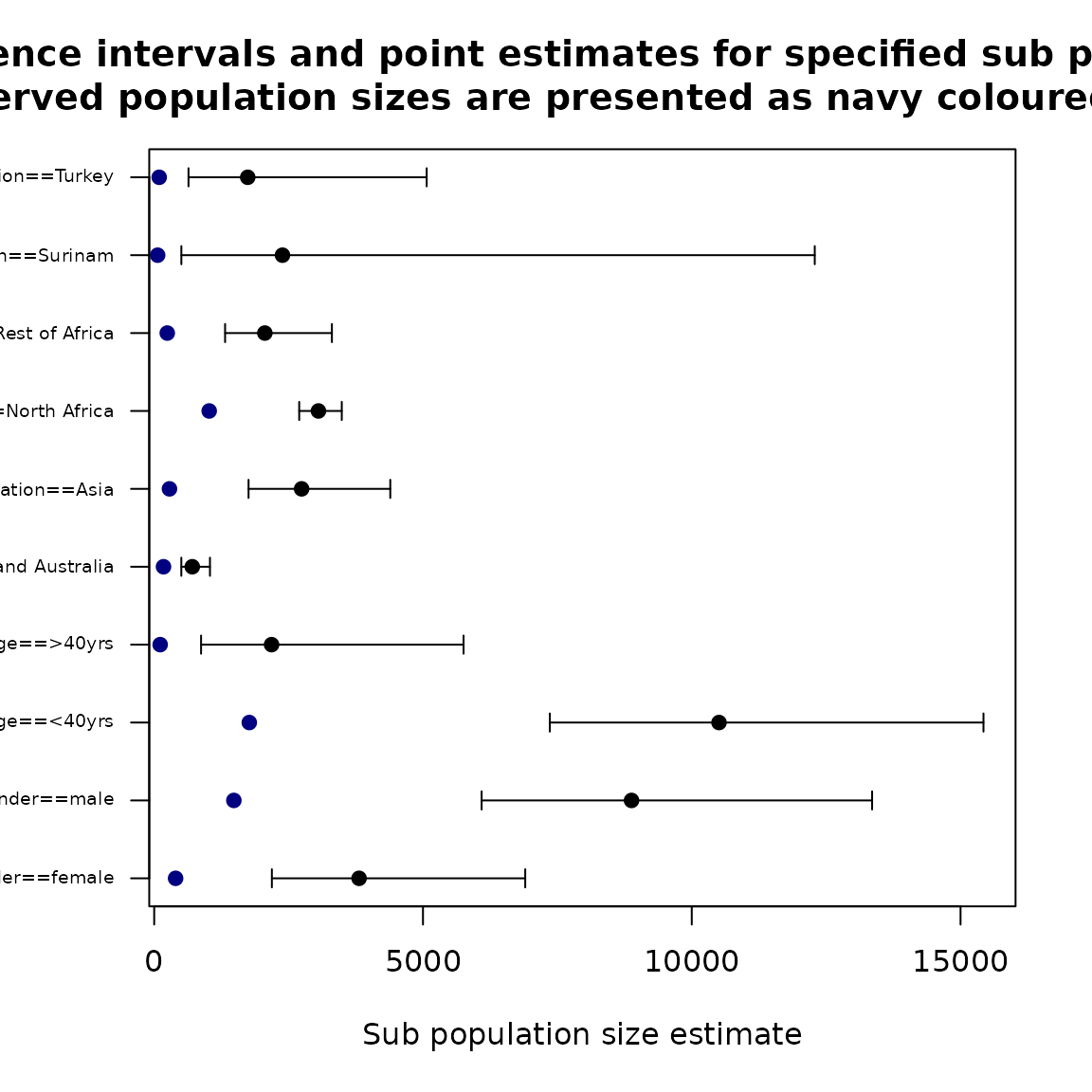
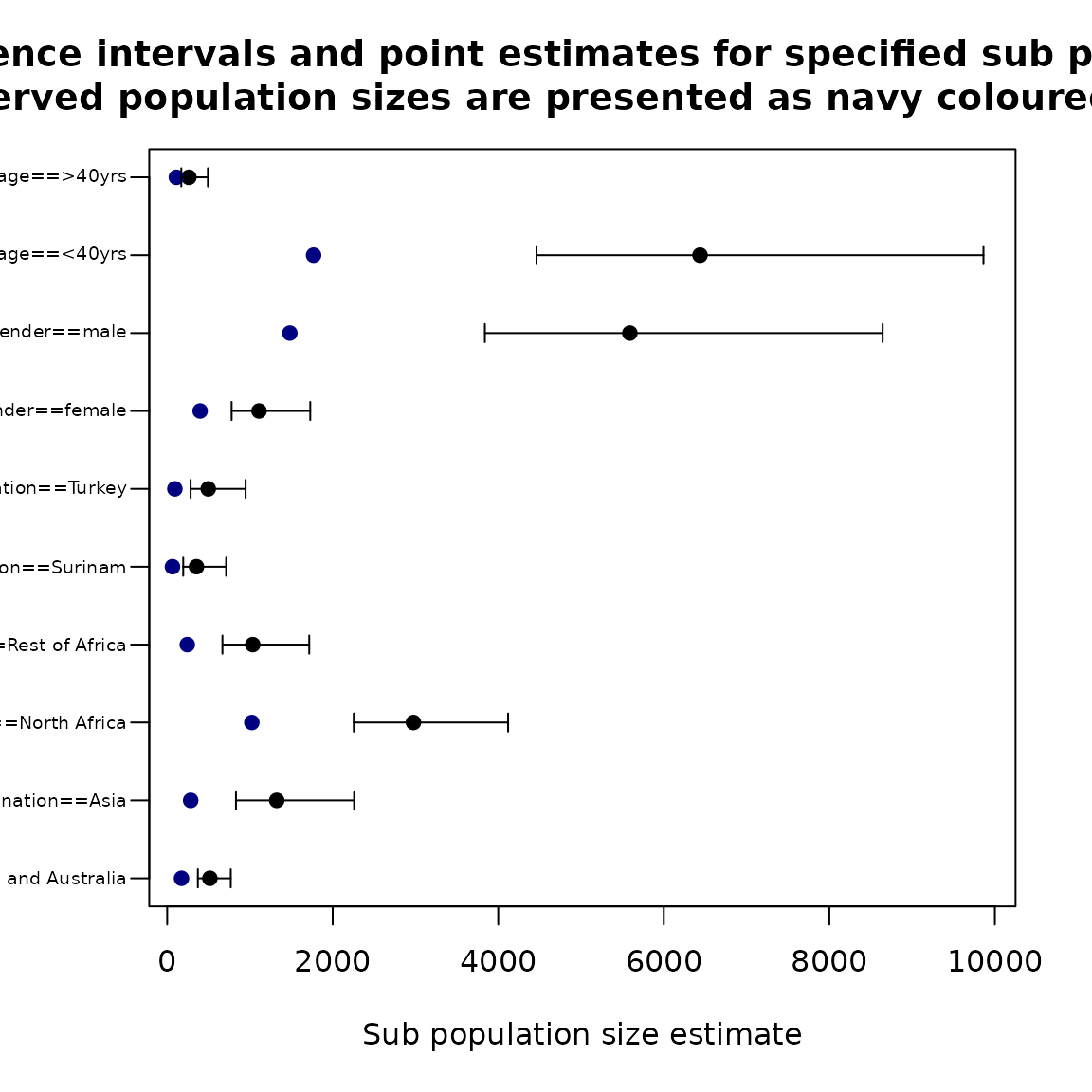
Population size by covariates for ztpoisson (left) and oiztgeom (right) model

Only the logNormal type of confidence interval is used for plotting since the studentized confidence intervals often result in negative lower bounds.

Classes and S3Methods

We have created a number of classes. The main ones are: singleRStaticCountData, singleRfamily, and supplementary are: popSizeEstResults, summarysingleRmargin and summarysingleRStaticCountData, which make it possible to extract relevant information regarding the population size.

For instance, the popSizeEst function can be used to extract information about the estimated size of the population as given below:

(popEst <- popSizeEst(basicModel))

## Point estimate: 12690.35
## Variance: 7885812
## 95% confidence intervals:
##           lowerBound upperBound
## normal      7186.444   18194.26
## logNormal   8431.275   19718.32

and the resulting object popEst of the popSizeEstResults class contains the following fields:

• pointEstimate, variance – numerics containing the point estimate and variance of this estimate.
• confidenceInterval – a data.frame with confidence intervals.
• boot – If the bootstrap was performed a numeric vector containing the $\hat{N}$ values from the bootstrap, a character vector with value "No bootstrap performed" otherwise.
• control – a controlPopVar object with controls used to obtain the object.

The only explicitly defined method for popSizeEstResults, summarysingleRmargin and summarysingleRStaticCountData classes is the print method, but the former one also accepts R primitives like coef:

coef(summary(basicModel))

##                        Estimate Std. Error    z value      P(>|z|)
## (Intercept)          -1.3410661  0.2148870 -6.2407965 4.353484e-10
## gendermale            0.3971793  0.1630155  2.4364504 1.483220e-02
## age>40yrs            -0.9746058  0.4082420 -2.3873235 1.697155e-02
## nationAsia           -1.0925990  0.3016259 -3.6223642 2.919228e-04
## nationNorth Africa    0.1899980  0.1940007  0.9793677 3.273983e-01
## nationRest of Africa -0.9106361  0.3008092 -3.0272880 2.467587e-03
## nationSurinam        -2.3363962  1.0135645 -2.3051282 2.115939e-02
## nationTurkey         -1.6753917  0.6027744 -2.7794674 5.444812e-03

analogously to glm from stats. The singleRfamily inherits the family class from stats and has explicitly defined print and simulate methods. Example usage is presented below

Function	Description
fitted	It works almost exactly like glm counterparts but returns more information, namely on fitted values for the truncated and non-truncated probability distribution;
logLik	Compared to glm method, it has the possibility of returning not just the value of the fitted log-likelihood but also the entire function (argument type = "function") along with two first derivatives (argument deriv = 0:2);
model.matrix	It has the possibility of returning the $X_{\text{vlm}}$ matrix defined previously;
simulate	It calls the simulate method for the chosen model and fitted $\boldsymbol{\eta}$;
predict	It has the possibility of returning either fitted distribution parameters for each unit (type = "response"), or just linear predictors (type = "link"), or means of the fitted distributions of $Y$ and $Y|Y>0$ (type = "mean") or the inverse probability weights (type = "contr"). It is possible to set the se.fit argument to TRUE in order to obtain standard errors for each of those by using the $\delta$ method. Also, it is possible to use a custom covariance matrix for standard error computation (argument cov);
redoPopEstimation	A function that applies all post-hoc procedures that were performed (such as heteroscedastic consistent covariance matrix estimation via countreg) to estimate the population size and standard errors;
residuals	Used for obtaining residuals of several types, we refer interested readers to the manual ?singleRcapture:::residuals.singleRStaticCountData;
stratifyPopsize, summary	Compared to the glm class, summary has the possibility of adding confidence intervals to the coefficient matrix (argument confint = TRUE) and using a custom covariance matrix (argument cov = someMatrix);
plot	It has been discussed above;
popSizeEst	An extractor showcased above;
cooks.distance	It works only for single predictor models;
dfbeta, dfpopsize	Multi-threading in dfbeta is available and dfpopsize calls dfbeta if no dfbeta object was provided in the call;
bread, estfun, vcovHC	For (almost) full sandwich compatibility;
AIC, BIC, extractAIC, family, confint, df.residual, model.frame, hatvalues, nobs, print, sigma, influence, rstudent, rstandard	These work exactly like glm counterparts.

set.seed(1234567890)
N <- 10000
gender <- rbinom(N, 1, 0.2)
eta <- -1 + 0.5*gender
counts <- simulate(ztpoisson(), eta = cbind(eta), seed = 1)
summary(data.frame(gender, eta, counts))

##      gender            eta              counts      
##  Min.   :0.0000   Min.   :-1.0000   Min.   :0.0000  
##  1st Qu.:0.0000   1st Qu.:-1.0000   1st Qu.:0.0000  
##  Median :0.0000   Median :-1.0000   Median :0.0000  
##  Mean   :0.2036   Mean   :-0.8982   Mean   :0.4196  
##  3rd Qu.:0.0000   3rd Qu.:-1.0000   3rd Qu.:1.0000  
##  Max.   :1.0000   Max.   :-0.5000   Max.   :5.0000

The full list of explicitly defined methods for singleRStaticCountData methods is presented in Table above.

Concluding remarks

In this paper we have introduced the singleRcapture package for single source capture-recapture models. The package implement state-of-the-art methods for estimating population size based on a single data set with multiple counts. The package implements different methods to account for heterogeneity in capture probabilities, modelled using covariates, as well as behavioural change, modelled using one-inflation. We have built the package to facilitate the implementation of new models using family objects; their application is exemplified in the Section 7. An example of implementing a custom family described in Section 8 is presented in replication materials.

Furthermore, since many R users are familiar with countreg or VGAM packages, we have implemented a lightweight extension called singleRcaptureExtra, available through Github (), which can be used to integrate singleRcapture with these packages.

In future work we plan to implement Bayesian estimation using Stan (e.g. via the brms package; Carpenter et al. (2017), Bürkner (2017)) and for one-inflation models we can use the recent approach proposed by Tuoto, Di Cecco, and Tancredi (2022) and implement our own families using the brms package.

Acknowledgements

The authors’ work has been financed by the National Science Centre in Poland, OPUS 20, grant no. 2020/39/B/HS4/00941.

The authors would like to thank Peter van der Heijden, Maarten Cruyff, Dankmar Böhning, Łukasz Chrostowski and Layna Dennett for useful comments that have helped to improve the functionality of the package. In addition, we would like to thank Marcin Szymkowiak and Tymon Świtalski for their valuable comments that have considerably improved the paper.

Detailed information

The estimatePopsizeFit function

In this section we provide a step-by-step description of how to prepare data in order to use the estimatePopsizeFit function, which may be useful to some users, e.g. those wishing to make modifications to the $\hat{N}$ estimate or to the bootstrap. In order to show how to apply the function we will fit a zero truncated geometric model on the data from Böhning et al. (2013) with covariate dependency:

$$\begin{align*} \log(\lambda) &= \beta_{1, 1} + \beta_{1, 2} \text{log\_distance} + \beta_{1, 3} \text{C\_TYPE} + \beta_{1, 4} \text{log\_size}, \\ \text{logit}(\omega) &= \beta_{2, 1} + \beta_{2, 2} \text{log\_distance} + \beta_{2, 3} \text{C\_TYPE}. \end{align*}$$

This would be equivalent to the following esimatePopsize call:

estimatePopsize(
  TOTAL_SUB ~ .,
  data = farmsubmission,
  model = ztoigeom(),
  controlModel(
    omegaFormula = ~ 1 + log_size + C_TYPE
  )
)

1. Create a data matrix $\boldsymbol{X}_{\text{vlm}}$

X <- matrix(data = 0, nrow = 2 * NROW(farmsubmission), ncol = 7)

2. Fill the first $n$ rows with model.matrix according to the specified formula and specify the attribute attr(X, "hwm") that informs the function which elements of the design matrix correspond to which linear predictor (covariates for counts and covariates for one-inflation)

X[1:NROW(farmsubmission), 1:4] <- model.matrix(
  ~ 1 + log_size + log_distance + C_TYPE, 
  farmsubmission
)
X[-(1:NROW(farmsubmission)), 5:7] <- model.matrix(
  ~ 1 + log_distance + C_TYPE, 
  farmsubmission
)
attr(X, "hwm") <- c(4, 3)

3. Obtain starting $\boldsymbol{\beta}$ parameters using the glm.fit function.

start <- glm.fit(
  y = farmsubmission$TOTAL_SUB, 
  x = X[1:NROW(farmsubmission), 1:4], 
  family = poisson()
)$coefficients
start

## [1] -0.82583943  0.33254499 -0.03277732  0.32746933

4. Use the estimatePopsizeFit function to fit the model assuming a zero-truncated one-inflated geometric distribution as specified in the family argument.

res <- estimatePopsizeFit(
  y            = farmsubmission$TOTAL_SUB, 
  X            = X, 
  method       = "IRLS", 
  priorWeights = 1, 
  family       = ztoigeom(), 
  control      = controlMethod(silent = TRUE), 
  coefStart    = c(start, 0, 0, 0),
  etaStart     = matrix(X %*% c(start, 0, 0, 0), ncol = 2),
  offset       = cbind(rep(0, NROW(farmsubmission)), 
                       rep(0, NROW(farmsubmission)))
)

5. Compare our results with those obtained by applying the stats::optim function.

ll <- ztoigeom()$makeMinusLogLike(y = farmsubmission$TOTAL_SUB, X = X)

res2 <- estimatePopsizeFit(
  y = farmsubmission$TOTAL_SUB, 
  X = X, 
  method = "optim", 
  priorWeights = 1, 
  family = ztoigeom(), 
  coefStart = c(start, 0, 0, 0),
  control = controlMethod(silent = TRUE, maxiter = 10000),
  offset = cbind(rep(0, NROW(farmsubmission)), rep(0, NROW(farmsubmission)))
)

data.frame(IRLS  = round(c(res$beta, -ll(res$beta), res$iter), 4),
           optim = round(c(res2$beta, -ll(res2$beta), res2$iter[1]), 4))

##          IRLS       optim
## 1     -2.7845     -2.5971
## 2      0.6170      0.6163
## 3     -0.0646     -0.0825
## 4      0.5346      0.5431
## 5     -3.1745     -0.1504
## 6      0.1281     -0.1586
## 7     -1.0865     -1.0372
## 8 -17278.7613 -17280.1189
## 9     15.0000   1696.0000

The default maxiter parameter for "optim" fitting is $1000$, but we needed to increase it since the optim does not converge in $1000$ steps and “gets stuck” at a plateau, which results in a lower log-likelihood value compared to the standard "IRLS".

The above situation is rather typical. While we did not conduct any formal numerical analyses, it seems that when one attempts to model more than one parameter of the distribution as covariate dependent optim algorithms, both "Nelder-Mead" and "L-BFGS-B" seem to be ill-suited for the task despite being provided with the analytically computed gradient. This is one of the reasons why "IRLS" is the default fitting method.

Structure of a family function

In this section we provide details regarding the family object for the singleRcapture package. This object contains additional parameters in comparison to the standard family object from the stats package.

Function	Description
makeMinusLogLike	A factory function for creating the following functions: $\ell(\boldsymbol{\beta})$, $\frac{\partial\ell}{\partial\boldsymbol{\beta}}$, $\frac{\partial^{2}\ell}{\partial\boldsymbol{\beta}^\top\partial\boldsymbol{\beta}}$ from the $\boldsymbol{y}$ vector and the $\boldsymbol{X}_{vlm}$ matrix. The deriv argument has possible values in c(0, 1, 2) that determine which derivative to return; the default value is 0, which represents the minus log-likelihood.
links	A list with link functions;
mu.eta, variance	Functions of linear predictors that return the expected value and variance. The type argument with 2 possible values ("trunc" and "nontrunc") specifies whether to return $\mathbb{E}[Y|Y>0], \text{var}[Y|Y>0]$ or $\mathbb{E}[Y], \text{var}[Y]$ respectively. The deriv argument with values in c(0, 1, 2) is used for indicating the derivative with respect to the linear predictors, which is used for providing standard errors in the predict method.
family	A string that specifies the model name;
valideta, validmu	For now, it only returns TRUE. In the near future, it will be used to check whether applied linear predictors are valid (i.e., are transformed into some elements of the parameter space subjected to the inverse link function).
funcZ, Wfun	Functions that create pseudo residuals and working weights used in the IRLS algorithm;
devResids	A function that returns deviance residuals given a vector of prior weights of linear predictors and the response vector;
pointEst, popVar	Functions that return the point estimate for the population size and analytic estimation of its variance given prior weights of linear predictors and, in the latter case, also estimates of $\text{cov}(\hat{\boldsymbol{\beta}})$ and $\boldsymbol{X}_{\text{vlm}}$ matrix. There is an additional boolean parameter contr in the former function, which, if set to TRUE, returns the contribution of each unit.
etaNames	Names of linear predictors;
densityFunction	A function that returns the value of PMF at values of x given linear predictors. The type argument specifies whether to return $\mathbb{P}[Y|Y>0]$ or $\mathbb{P}[Y]$;
simulate	A function that generates values of a dependent vector given linear predictors;
getStart	An expression for generating starting points;

Implementing a custom singleRcapture family function

Suppose we want to implement a very specific zero truncated family function in the singleRcapture, which corresponds to the following “untruncated” distribution:

$$\mathbb{P}[Y=y|\lambda, \pi] = \begin{cases} 1 - \frac{1}{2}\lambda - \frac{1}{2}\pi & \text{when: } y=0\\ \frac{1}{2}\pi & \text{when: } y=1\\ \frac{1}{2}\lambda & \text{when: } y=2, \end{cases}$$

with $\lambda, \pi\in\left(0, 1\right)$ being dependent on covariates.

Below we provide a possible way of implementing the above model, with lambda, pi meaning $\frac{1}{2}\lambda,\frac{1}{2}\pi$. We provide a simple example that shows that the proposed approach works as expected.

myFamilyFunction <- function(lambdaLink = c("logit", "cloglog", "probit"),
                             piLink     = c("logit", "cloglog", "probit"),
                             ...) {
  if (missing(lambdaLink)) lambdaLink <- "logit"
  if (missing(piLink))         piLink <- "logit"

  links <- list()
  attr(links, "linkNames") <- c(lambdaLink, piLink)

  lambdaLink <- switch(lambdaLink,
                       "logit"   = singleRcapture:::singleRinternallogitLink,
                       "cloglog" = singleRcapture:::singleRinternalcloglogLink,
                       "probit"  = singleRcapture:::singleRinternalprobitLink
  )

  piLink <- switch(piLink,
                   "logit"   = singleRcapture:::singleRinternallogitLink,
                   "cloglog" = singleRcapture:::singleRinternalcloglogLink,
                   "probit"  = singleRcapture:::singleRinternalprobitLink
  )

  links[1:2] <- c(lambdaLink, piLink)

  mu.eta <- function(eta, type = "trunc", deriv = FALSE, ...) {
    pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
    lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2

    if (!deriv) {
      switch (type,
              "nontrunc" = pi + 2 * lambda,
              "trunc" = 1 + lambda / (pi + lambda)
      )
    } else {
      # Only necessary if one wishes to use standard errors in predict method
      switch (type,
              "nontrunc" = {
                matrix(c(2, 1) * c(
                  lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) / 2,
                  piLink(eta[, 2], inverse = TRUE, deriv = 1) / 2
                ), ncol = 2)
              },
              "trunc" = {
                matrix(c(
                  pi / (pi + lambda) ^ 2,
                  -lambda / (pi + lambda) ^ 2
                ) * c(
                  lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) / 2,
                  piLink(eta[, 2], inverse = TRUE, deriv = 1) / 2
                ), ncol = 2)
              }
      )
    }
  }

  variance <- function(eta, type = "nontrunc", ...) {
    pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
    lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2

    switch (type,
            "nontrunc" = pi * (1 - pi) + 4 * lambda * (1 - lambda - pi),
            "trunc" = lambda * (1 - lambda) / (pi + lambda)
    )
  }

  Wfun <- function(prior, y, eta, ...) {
    pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
    lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2

    G01 <- ((lambda + pi) ^ (-2)) * piLink(eta[, 2], inverse = TRUE, deriv = 1) *
      lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) * prior / 4

    G00 <- ((lambda + pi) ^ (-2)) - (pi ^ (-2)) - lambda / ((lambda + pi) * (pi ^ 2))
    G00 <- G00 * prior * (piLink(eta[, 2], inverse = TRUE, deriv = 1) ^ 2) / 4

    G11 <- ((lambda + pi) ^ (-2)) - (((lambda + pi) * lambda) ^ -1)
    G11 <- G11 * prior * (lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) ^ 2) / 4

    matrix(
      -c(G11, # lambda
         G01, # mixed
         G01, # mixed
         G00  # pi
      ),
      dimnames = list(rownames(eta), c("lambda", "mixed", "mixed", "pi")),
      ncol = 4
    )
  }

  funcZ <- function(eta, weight, y, prior, ...) {
    pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
    lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2

    weight <- weight / prior

    G0 <- (2 - y) / pi     - ((lambda + pi) ^ -1)
    G1 <- (y - 1) / lambda - ((lambda + pi) ^ -1)

    G1 <- G1 * lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) / 2
    G0 <- G0 *     piLink(eta[, 2], inverse = TRUE, deriv = 1) / 2

    uMatrix <- matrix(c(G1, G0), ncol = 2)

    weight <- lapply(X = 1:nrow(weight), FUN = function (x) {
      matrix(as.numeric(weight[x, ]), ncol = 2)
    })

    pseudoResid <- sapply(X = 1:length(weight), FUN = function (x) {
      #xx <- chol2inv(chol(weight[[x]])) # less computationally demanding
      xx <- solve(weight[[x]]) # more stable
      xx %*% uMatrix[x, ]
    })
    pseudoResid <- t(pseudoResid)
    dimnames(pseudoResid) <- dimnames(eta)
    pseudoResid
  }

  minusLogLike <- function(y, X, offset,
                           weight    = 1,
                           NbyK      = FALSE,
                           vectorDer = FALSE,
                           deriv     = 0,
                           ...) {
    y <- as.numeric(y)
    if (is.null(weight)) {
      weight <- 1
    }
    if (missing(offset)) {
      offset <- cbind(rep(0, NROW(X) / 2), rep(0, NROW(X) / 2))
    }

    if (!(deriv %in% c(0, 1, 2)))
      stop("Only score function and derivatives up to 2 are supported.")
    deriv <- deriv + 1

    switch (deriv,
            function(beta) {
              eta <- matrix(as.matrix(X) %*% beta, ncol = 2) + offset
              pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
              lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2
              -sum(weight * ((2 - y) * log(pi) + (y - 1) * log(lambda) - log(pi + lambda)))
            },
            function(beta) {
              eta <- matrix(as.matrix(X) %*% beta, ncol = 2) + offset
              pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
              lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2

              G0 <- (2 - y) / pi     - ((lambda + pi) ^ -1)
              G1 <- (y - 1) / lambda - ((lambda + pi) ^ -1)

              G1 <- G1 * weight * lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) / 2
              G0 <- G0 * weight *     piLink(eta[, 2], inverse = TRUE, deriv = 1) / 2

              if (NbyK) {
                XX <- 1:(attr(X, "hwm")[1])
                return(cbind(as.data.frame(X[1:nrow(eta), XX]) * G1,
                             as.data.frame(X[-(1:nrow(eta)), -XX]) * G0))
              }
              if (vectorDer) {
                return(cbind(G1, G0))
              }

              as.numeric(c(G1, G0) %*% X)
            },
            function (beta) {
              lambdaPredNumber <- attr(X, "hwm")[1]
              eta <- matrix(as.matrix(X) %*% beta, ncol = 2) + offset
              pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
              lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2

              res <- matrix(nrow = length(beta), ncol = length(beta),
                            dimnames = list(names(beta), names(beta)))

              # pi^2 derivative
              dpi <- (2 - y) / pi - (lambda + pi) ^ -1
              G00 <- ((lambda + pi) ^ (-2)) - (2 - y) / (pi ^ 2)

              G00 <- t(as.data.frame(X[-(1:(nrow(X) / 2)), -(1:lambdaPredNumber)] *
                                       (G00 * ((piLink(eta[, 2], inverse = TRUE, deriv = 1) / 2) ^ 2) +
                                          dpi * piLink(eta[, 2], inverse = TRUE, deriv = 2) / 2) * weight)) %*%
                as.matrix(X[-(1:(nrow(X) / 2)), -(1:lambdaPredNumber)])
              # mixed derivative
              G01 <- (lambda + pi) ^ (-2)

              G01 <- t(as.data.frame(X[1:(nrow(X) / 2), 1:lambdaPredNumber]) *
                         G01 * (lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) / 2) *
                         (piLink(eta[, 2], inverse = TRUE, deriv = 1) / 2) * weight) %*%
                as.matrix(X[-(1:(nrow(X) / 2)), -(1:lambdaPredNumber)])
              # lambda^2 derivative
              G11 <- ((lambda + pi) ^ (-2)) - (y - 1) / (lambda ^ 2)
              dlambda <- (y - 1) / lambda - ((lambda + pi) ^ -1)

              G11 <- t(as.data.frame(X[1:(nrow(X) / 2), 1:lambdaPredNumber] *
                                       (G11 * ((lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) / 2) ^ 2) +
                                          dlambda * lambdaLink(eta[, 1], inverse = TRUE, deriv = 2) / 2) * weight)) %*%
                X[1:(nrow(X) / 2), 1:lambdaPredNumber]

              res[-(1:lambdaPredNumber), -(1:lambdaPredNumber)] <- G00
              res[1:lambdaPredNumber, 1:lambdaPredNumber] <- G11
              res[1:lambdaPredNumber, -(1:lambdaPredNumber)] <- t(G01)
              res[-(1:lambdaPredNumber), 1:lambdaPredNumber] <- G01

              res
            }
    )
  }

  validmu <- function(mu) {
    (sum(!is.finite(mu)) == 0) && all(0 < mu) && all(2 > mu)
  }

  # this is optional
  devResids <- function(y, eta, wt, ...) {
    0
  }

  pointEst <- function (pw, eta, contr = FALSE, ...) {
    pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
    lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2
    N <- pw / (lambda + pi)
    if(!contr) {
      N <- sum(N)
    }
    N
  }

  popVar <- function (pw, eta, cov, Xvlm, ...) {
    pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
    lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2

    bigTheta1 <- -pw / (pi + lambda) ^ 2 # w.r to pi
    bigTheta1 <- bigTheta1 * piLink(eta[, 2], inverse = TRUE, deriv = 1) / 2
    bigTheta2 <- -pw / (pi + lambda) ^ 2 # w.r to lambda
    bigTheta2 <- bigTheta2 * lambdaLink(eta[, 1], inverse = TRUE, deriv = 1) / 2 # w.r to lambda

    bigTheta <- t(c(bigTheta2, bigTheta1) %*% Xvlm)

    f1 <- t(bigTheta) %*% as.matrix(cov) %*% bigTheta

    f2 <- sum(pw * (1 - pi - lambda) / ((pi + lambda) ^ 2))

    f1 + f2
  }

  dFun <- function (x, eta, type = c("trunc", "nontrunc")) {
    if (missing(type)) type <- "trunc"
    pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
    lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2

    switch (type,
            "trunc" = {
              (pi * as.numeric(x == 1) + lambda * as.numeric(x == 2)) / (pi + lambda)
            },
            "nontrunc" = {
              (1 - pi - lambda) * as.numeric(x == 0) +
                pi * as.numeric(x == 1) + lambda * as.numeric(x == 2)
            }
    )
  }

  simulate <- function(n, eta, lower = 0, upper = Inf) {
    pi     <-     piLink(eta[, 2], inverse = TRUE) / 2
    lambda <- lambdaLink(eta[, 1], inverse = TRUE) / 2
    CDF <- function(x) {
      ifelse(x == Inf, 1,
             ifelse(x < 0, 0,
                    ifelse(x < 1, 1 - pi - lambda,
                           ifelse(x < 2, 1 - lambda, 1))))
    }
    lb <- CDF(lower)
    ub <- CDF(upper)
    p_u <- stats::runif(n, lb, ub)
    sims <- rep(0, n)
    cond <- CDF(sims) <= p_u
    while (any(cond)) {
      sims[cond] <- sims[cond] + 1
      cond <- CDF(sims) <= p_u
    }
    sims
  }

  getStart <- expression(
    if (method == "IRLS") {
      etaStart <- cbind(
        family$links[[1]](mean(observed == 2) * (1 + 0 * (observed == 2))), # lambda
        family$links[[2]](mean(observed == 1) * (1 + 0 * (observed == 1)))  # pi
      ) + offset
    } else if (method == "optim") {
      init <- c(
        family$links[[1]](weighted.mean(observed == 2, priorWeights) * 1 + .0001),
        family$links[[2]](weighted.mean(observed == 1, priorWeights) * 1 + .0001)
      )
      if (attr(terms, "intercept")) {
        coefStart <- c(init[1], rep(0, attr(Xvlm, "hwm")[1] - 1))
      } else {
        coefStart <- rep(init[1] / attr(Xvlm, "hwm")[1], attr(Xvlm, "hwm")[1])
      }
      if ("(Intercept):pi" %in% colnames(Xvlm)) {
        coefStart <- c(coefStart, init[2], rep(0, attr(Xvlm, "hwm")[2] - 1))
      } else {
        coefStart <- c(coefStart, rep(init[2] / attr(Xvlm, "hwm")[2], attr(Xvlm, "hwm")[2]))
      }
    }
  )

  structure(
    list(
      makeMinusLogLike = minusLogLike,
      densityFunction  = dFun,
      links     = links,
      mu.eta    = mu.eta,
      valideta  = function (eta) {TRUE},
      variance  = variance,
      Wfun      = Wfun,
      funcZ     = funcZ,
      devResids = devResids,
      validmu   = validmu,
      pointEst  = pointEst,
      popVar    = popVar,
      family    = "myFamilyFunction",
      etaNames  = c("lambda", "pi"),
      simulate  = simulate,
      getStart  = getStart,
      extraInfo = c(
        mean       = "pi / 2 + lambda",
        variance   = paste0("(pi / 2) * (1 - pi / 2) + 2 * lambda * (1 - lambda / 2 - pi / 2)"),
        popSizeEst = "(1 - (pi + lambda) / 2) ^ -1",
        meanTr     = "1 + lambda / (pi + lambda)",
        varianceTr = paste0("lambda * (1 - lambda / 2) / (pi + lambda)")
      )
    ),
    class = c("singleRfamily", "family")
  )
}

A quick tests shows us that this implementation in fact works:

set.seed(123)
Y <- simulate(
  myFamilyFunction(lambdaLink = "logit", piLink = "logit"),
  nsim = 1000, eta = matrix(0, nrow = 1000, ncol = 2),
  truncated = FALSE
)
mm <- estimatePopsize(
  formula = Y ~ 1,
  data = data.frame(Y = Y[Y > 0]),
  model = myFamilyFunction(lambdaLink = "logit",
                           piLink = "logit"),
  # the usual observed information matrix
  # is ill-suited for this distribution
  controlPopVar = controlPopVar(covType = "Fisher")
)
summary(mm)

## 
## Call:
## estimatePopsize.default(formula = Y ~ 1, data = data.frame(Y = Y[Y > 
##     0]), model = myFamilyFunction(lambdaLink = "logit", piLink = "logit"), 
##     controlPopVar = controlPopVar(covType = "Fisher"))
## 
## Pearson Residuals:
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -0.8198 -0.8198  0.8099  0.0000  0.8099  0.8099 
## 
## Coefficients:
## -----------------------
## For linear predictors associated with: lambda 
##             Estimate Std. Error z value P(>|z|)
## (Intercept)  0.01217    0.20253    0.06   0.952
## -----------------------
## For linear predictors associated with: pi 
##             Estimate Std. Error z value P(>|z|)
## (Intercept) -0.01217    0.08926  -0.136   0.892
## 
## AIC: 687.4249
## BIC: 695.8259
## Residual deviance: 0
## 
## Log-likelihood: -341.7124 on 984 Degrees of freedom 
## Number of iterations: 2
## -----------------------
## Population size estimation results: 
## Point estimate 986
## Observed proportion: 50% (N obs = 493)
## Std. Error 70.30092
## 95% CI for the population size:
##           lowerBound upperBound
## normal      848.2127   1123.787
## logNormal   866.3167   1144.053
## 95% CI for the share of observed population:
##           lowerBound upperBound
## normal      43.86951   58.12221
## logNormal   43.09241   56.90759

where the link functions, such as singleRcapture:::singleRinternalcloglogLink, are just internal functions in singleRcapture that compute link functions, their inverses and derivatives of both links and inverse links up to the third order:

singleRcapture:::singleRinternalcloglogLink

## function (x, inverse = FALSE, deriv = 0) 
## {
##     deriv <- deriv + 1
##     if (isFALSE(inverse)) {
##         res <- switch(deriv, log(-log(1 - x)), -1/((1 - x) * 
##             log(1 - x)), -(1 + log(1 - x))/((x - 1)^2 * log(1 - 
##             x)^2), (2 * log(1 - x)^2 + 3 * log(1 - x) + 2)/(log(1 - 
##             x)^3 * (x - 1)^3))
##     }
##     else {
##         res <- switch(deriv, 1 - exp(-exp(x)), exp(x - exp(x)), 
##             (1 - exp(x)) * exp(x - exp(x)), (exp(2 * x) - 3 * 
##                 exp(x) + 1) * exp(x - exp(x)))
##     }
##     res
## }
## <bytecode: 0x55b303c0ea70>
## <environment: namespace:singleRcapture>

One could, of course, include the code for computing them manually.

References

Baffour, Bernard, Thomas King, and Paolo Valente. 2013. “The Modern Census: Evolution, Examples and Evaluation.” International Statistical Review 81 (3): 407–25. https://doi.org/10.1111/insr.12036.

Baillargeon, Sophie, and Louis-Paul Rivest. 2007. “Rcapture: Loglinear Models for Capture-Recapture in r.” Journal of Statistical Software 19 (5): 1–31. https://doi.org/10.18637/jss.v019.i05.

Besançon, Mathieu, Theodore Papamarkou, David Anthoff, Alex Arslan, Simon Byrne, Dahua Lin, and John Pearson. 2021. “Distributions.jl: Definition and Modeling of Probability Distributions in the JuliaStats Ecosystem.” Journal of Statistical Software 98 (16): 1–30. https://doi.org/10.18637/jss.v098.i16.

Böhning, Dankmar. 2023. “On the Equivalence of One-Inflated Zero-Truncated and Zero-Truncated One-Inflated Count Data Likelihoods.” Biometrical Journal 65 (2): 2100343. https://doi.org/10.1002/bimj.202100343.

Böhning, Dankmar, John Bunge, and Peter GM Heijden. 2018. Capture-Recapture Methods for the Social and Medical Sciences. CRC Press Boca Raton.

Böhning, Dankmar, and Herwig Friedl. 2021. “Population Size Estimation Based Upon Zero-Truncated, One-Inflated and Sparse Count Data: Estimating the Number of Dice Snakes in Graz and Flare Stars in the Pleiades.” Statistical Methods & Applications, January. https://doi.org/10.1007/s10260-021-00556-8.

———. 2024. “One-Inflation and Zero-Truncation Count Data Modelling Revisited with a View on Horvitz–Thompson Estimation of Population Size.” International Statistical Review 92 (1): 148–65. https://doi.org/10.1111/insr.12557.

Böhning, Dankmar, and Peter G. M. van der Heijden. 2009. “A Covariate Adjustment for Zero-Truncated Approaches to Estimating the Size of Hidden and Elusive Populations.” The Annals of Applied Statistics 3 (2): 595–610. https://doi.org/10.1214/08-AOAS214.

———. 2019. “The Identity of the Zero-Truncated, One-Inflated Likelihood and the Zero-One-Truncated Likelihood for General Count Densities with an Application to Drink-Driving in Britain.” The Annals of Applied Statistics 13 (2): 1198–1211. https://doi.org/10.1214/18-AOAS1232.

Böhning, Dankmar, Alberto Vidal-Diez, Rattana Lerdsuwansri, Chukiat Viwatwongkasem, and Mark Arnold. 2013. “A Generalization of Chao’s Estimator for Covariate Information.” Biometrics 69 (4): 1033–42. https://doi.org/10.1111/biom.12062.

Bürkner, Paul-Christian. 2017. “brms: An R Package for Bayesian Multilevel Models Using Stan.” Journal of Statistical Software 80 (1): 1–28. https://doi.org/10.18637/jss.v080.i01.

Carpenter, Bob, Andrew Gelman, Matthew D Hoffman, Daniel Lee, Ben Goodrich, Michael Betancourt, Marcus Brubaker, Jiqiang Guo, Peter Li, and Allen Riddell. 2017. “Stan: A Probabilistic Programming Language.” Journal of Statistical Software 76 (1): 1–32. https://doi.org/10.18637/jss.v076.i01.

Chao, Anne. 1987. “Estimating the Population Size for Capture-Recapture Data with Unequal Catchability.” Biometrics 43 (4): 783–91. https://doi.org/10.2307/2531532.

Cruyff, Maarten J. L. F., and Peter G. M. van der Heijden. 2008. “Point and Interval Estimation of the Population Size Using a Zero-Truncated Negative Binomial Regression Model.” Biometrical Journal 50 (6): 1035–50. https://doi.org/10.1002/bimj.200810455.

Dunne, John, and Li-Chun Zhang. 2024. “A System of Population Estimates Compiled from Administrative Data Only.” Journal of the Royal Statistical Society Series A: Statistics in Society 187 (1): 3–21. https://doi.org/10.1093/jrsssa/qnad067.

Godwin, Ryan T., and Dankmar Böhning. 2017a. “Estimation of the Population Size by Using the One-Inflated Positive Poisson Model.” Journal of the Royal Statistical Society Series C: Applied Statistics 66 (2): 425–48. https://doi.org/10.1111/rssc.12192.

Godwin, Ryan T, and Dankmar Böhning. 2017b. “Estimation of the Population Size by Using the One-Inflated Positive Poisson Model.” Journal of the Royal Statistical Society Series C: Applied Statistics 66 (2): 425–48. https://doi.org/10.1111/rssc.12192.

Hayes, Alex, Ralph Moller-Trane, Daniel Jordan, Paul Northrop, Moritz N. Lang, and Achim Zeileis. 2024. Distributions3: Probability Distributions as S3 Objects. https://CRAN.R-project.org/package=distributions3.

Heijden, Peter GM van der, Rami Bustami, Maarten JLF Cruyff, Godfried Engbersen, and Hans C van Houwelingen. 2003. “Point and Interval Estimation of the Population Size Using the Truncated Poisson Regression Model.” Statistical Modelling 3 (4): 305–22. https://doi.org/10.1191/1471082X03st057oa.

Kleiber, Christian, and Achim Zeileis. 2016. “Visualizing Count Data Regressions Using Rootograms.” The American Statistician 70 (3): 296–303. https://doi.org/10.1080/00031305.2016.1173590.

Laake, Jeff L, Devin S Johnson, Paul B Conn, and Nick Isaac. 2013. “Marked: An r Package for Maximum Likelihood and Markov Chain Monte Carlo Analysis of Capture-Recapture Data.” Methods in Ecology & Evolution 4 (9): 885–90. https://doi.org/10.1111/2041-210X.12065.

Microsoft, and Steve Weston. 2022a. doParallel: Foreach Parallel Adaptor for the ’Parallel’ Package. https://CRAN.R-project.org/package=doParallel.

———. 2022b. Foreach: Provides Foreach Looping Construct. https://CRAN.R-project.org/package=foreach.

Norris, James L, and Kenneth H Pollock. 1996. “Including Model Uncertainty in Estimating Variances in Multiple Capture Studies.” Environmental and Ecological Statistics 3 (3): 235–44. https://doi.org/10.1007/BF00569242.

R Core Team. 2023. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Seabold, Skipper, and Josef Perktold. 2010. “Statsmodels: Econometric and Statistical Modeling with Python.” In 9th Python in Science Conference.

Tuoto, Tiziana, Davide Di Cecco, and Andrea Tancredi. 2022. “Bayesian Analysis of One-Inflated Models for Elusive Population Size Estimation.” Biometrical Journal 64 (5): 912–33. https://doi.org/10.1002/bimj.202100048.

Vincent, Kyle, and Steve Thompson. 2022. “Estimating the Size and Distribution of Networked Populations with Snowball Sampling.” Journal of Survey Statistics and Methodology 10 (2): 397–418. https://doi.org/10.1093/jssam/smaa037.

Wolter, Kirk M. 1986. “Some Coverage Error Models for Census Data.” Journal of the American Statistical Association 81 (394): 337–46. https://doi.org/10.1080/01621459.1986.10478277.

Yang, Hsing-Chen, and Anne Chao. 2006. “Program CARE-4 (for Capture-Recapture Part. 4).” http://chao.stat.nthu.edu.tw.

Yee, Thomas. 2015. Vector Generalized Linear and Additive Models: With an Implementation in r. 1st ed. Springer Publishing Company, Incorporated.

Yee, Thomas W., and Chenchen Ma. 2024. “Generally Altered, Inflated, Truncated and Deflated Regression.” Statistical Science 39 (4): 568–88. https://doi.org/10.1214/24-STS925.

Yee, Thomas W, Jakub Stoklosa, and Richard M Huggins. 2015. “The VGAM Package for Capture-Recapture Data Using the Conditional Likelihood.” Journal of Statistical Software 65 (1): 1–33. https://doi.org/10.18637/jss.v065.i05.

Zeileis, Achim, and Torsten Hothorn. 2002. “Diagnostic Checking in Regression Relationships.” R News 2 (3): 7–10. https://CRAN.R-project.org/doc/Rnews/.

Zeileis, Achim, Christian Kleiber, and Simon Jackman. 2008. “Regression Models for Count Data in R.” Journal of Statistical Software 27 (8): 1–25. https://doi.org/10.18637/jss.v027.i08.

Zeileis, Achim, Susanne Köll, and Nathaniel Graham. 2020. “Various Versatile Variances: An Object-Oriented Implementation of Clustered Covariances in R.” Journal of Statistical Software 95 (1): 1–36. https://doi.org/10.18637/jss.v095.i01.

Zelterman, Daniel. 1988. “Robust Estimation in Truncated Discrete Distributions with Application to Capture-Recapture Experiments.” Journal of Statistical Planning and Inference 18 (2): 225–37. https://doi.org/10.1016/0378-3758(88)90097-9.

Zhang, Li-Chun. 2019. “A Note on Dual System Population Size Estimator.” Journal of Official Statistics 35 (1): 279–83. https://doi.org/10.2478/jos-2019-0013.

Zwane, EN, and PGM Van der Heijden. 2003. “Implementing the Parametric Bootstrap in Capture–Recapture Models with Continuous Covariates.” Statistics & Probability Letters 65 (2): 121–25. https://doi.org/10.1016/j.spl.2003.07.003.